Pentacubits – Die Spielsteine
Pentacubits – ein Puzzle auf Basis einer Raute
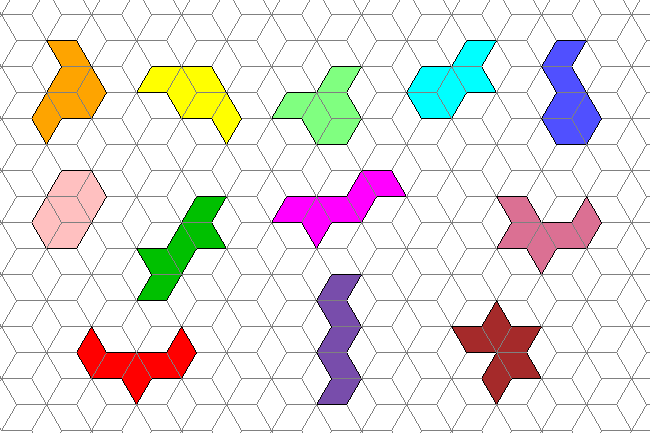
Jedes der 12 Pentacubits besteht aus 5 Rauten. Die Pentacubits gehören zur Familie der Polycubits.
Die Grundform der Polycubits ist eine Raute mit zwei 60°- und zwei 120°-Innenwinkeln. Diese Rauten fügen sich nahtlos in das gezeigte Wabengitter ein.
Es gibt: 1 Dicubit, 3 Tricubits, 4 Tetracubits, 12 Pentacubits, 27 Hexacubits, 78 Heptacubits.
Pentacubits-Puzzles
Symmetrische Figuren aus Pentacubits
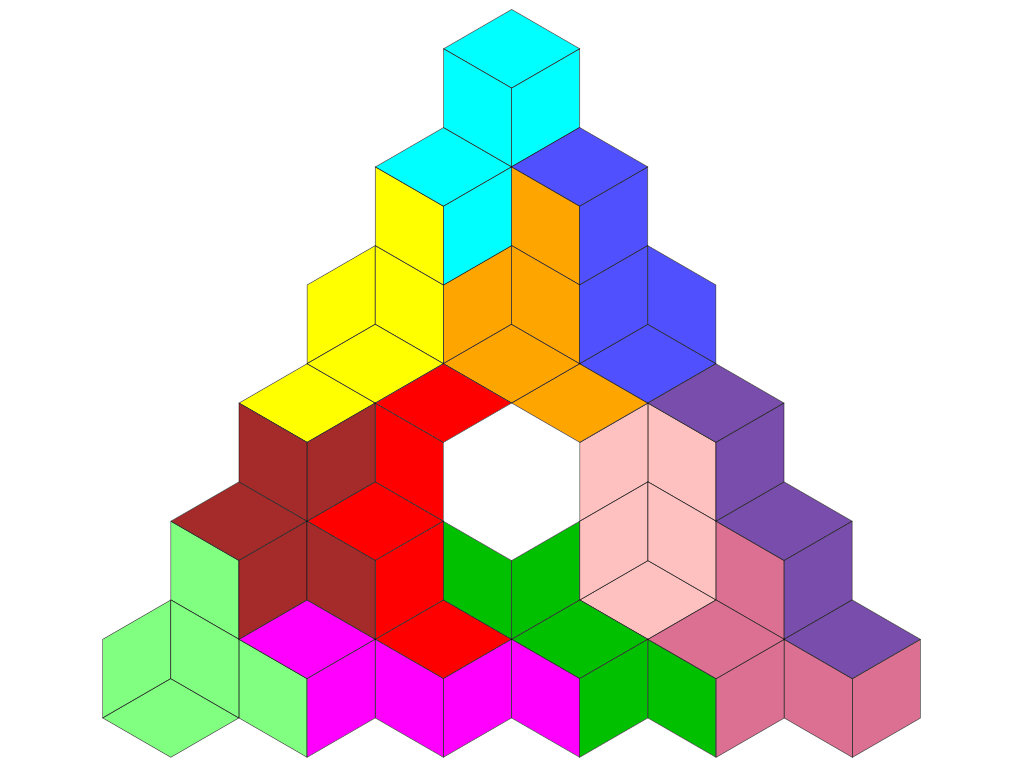
Figuren aus den 12 Pentacubits bedecken eine Fläche von 60 Rauten. Für ein lückenloses, gleichseitiges Dreieck mit vollständiger Füllung werden jedoch 63 Rauten benötigt. Deshalb wurde das Puzzle für die 3D-Druck-Variante um ein zusätzliches Tricubit ergänzt.
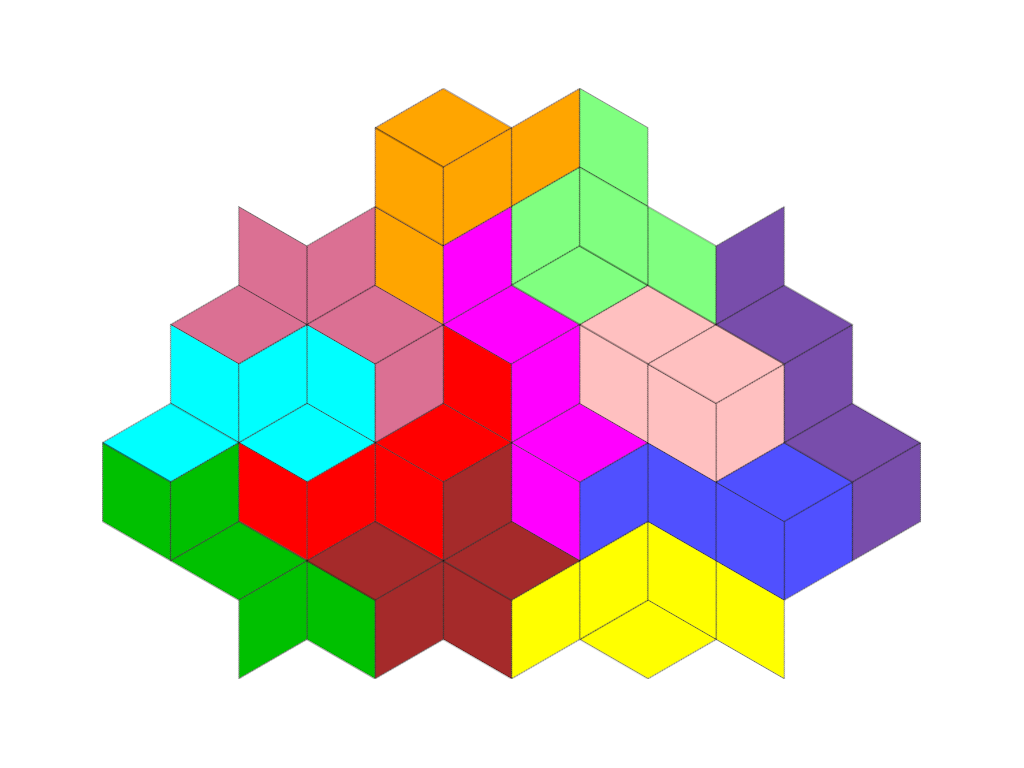
Das zugrunde liegende Wabengitter erlaubt Figuren mit sechs Spiegelachsen und sechsfacher Drehsymmetrie. Vollsymmetrische Figuren, die ausschließlich aus den 12 Pentacubits bestehen, sind jedoch (vermutlich) nicht möglich.
Das Puzzle wurde mit Unterstützung des Programms PolySolver entwickelt..
Einige Figuren aus Pentacubits
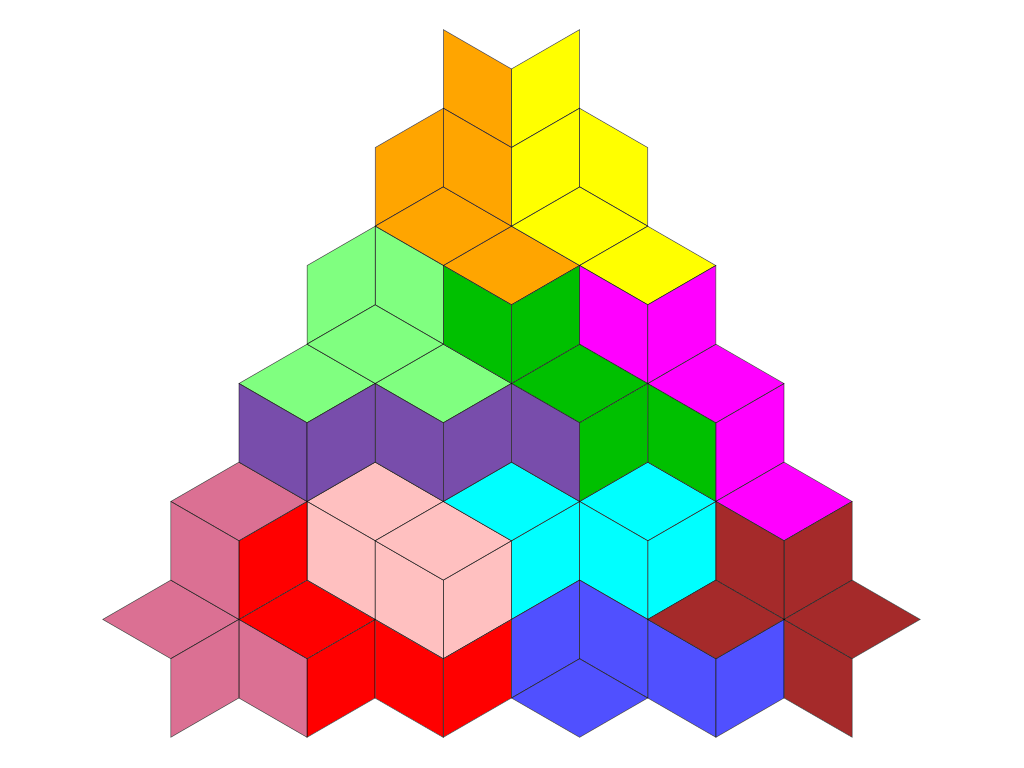
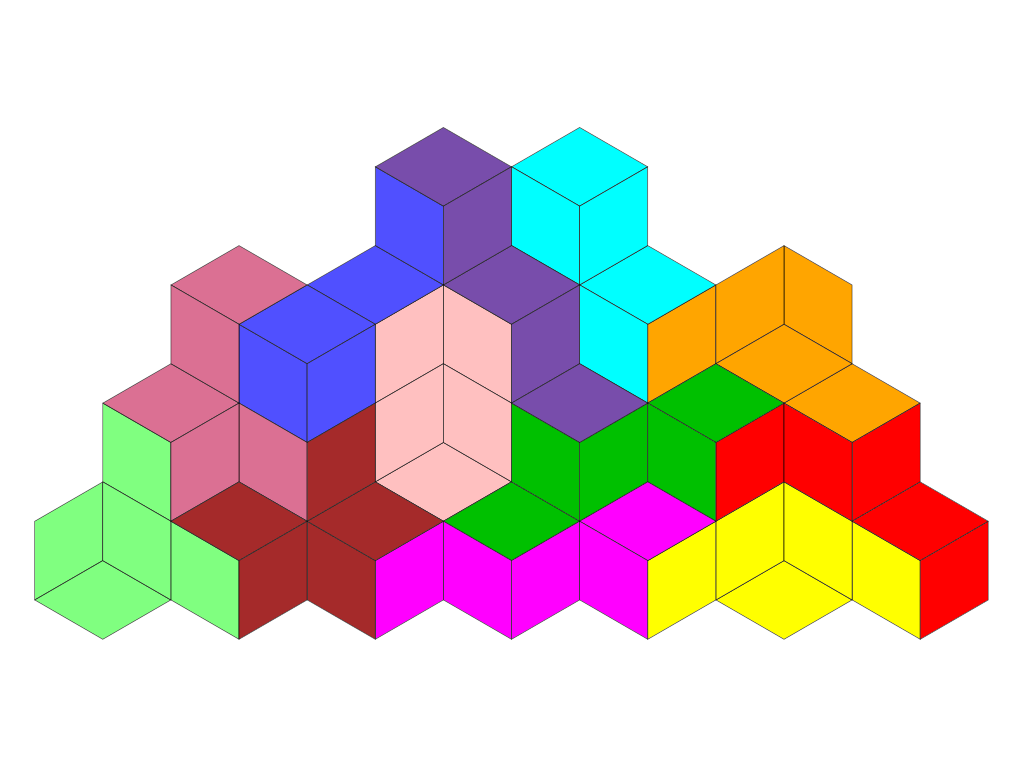
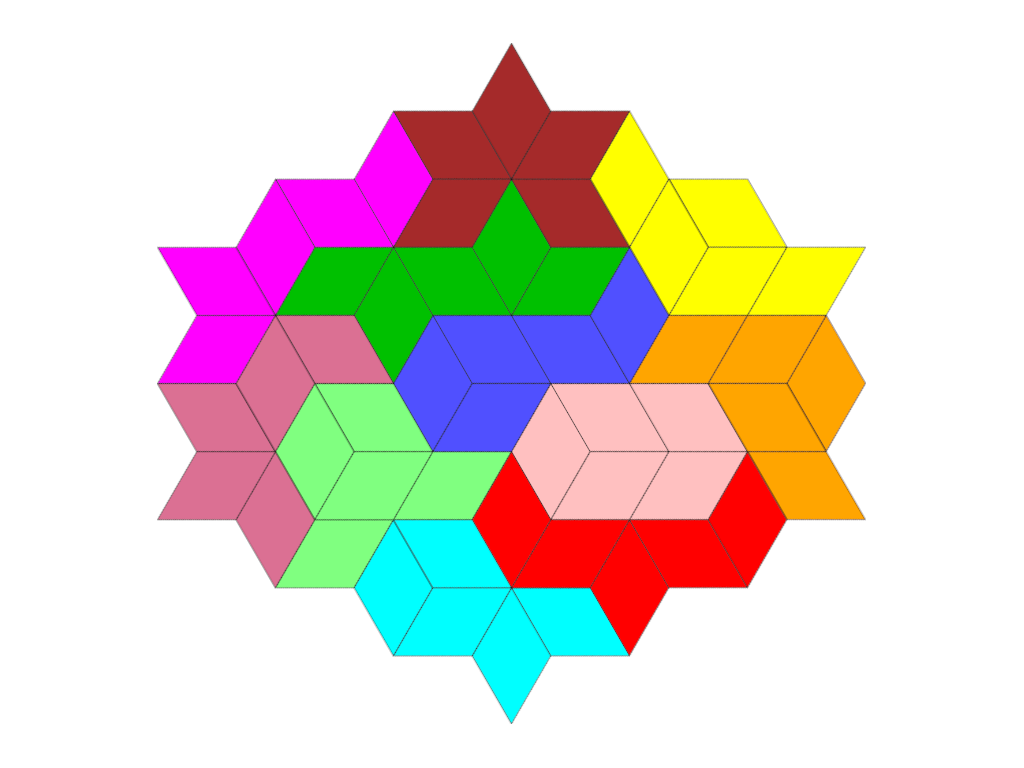
Ressourcen & Downloads
3D-Druck-Vorlagen
Die 3D-Druckvorlagen bestehen aus den 12 Pentacubits und einer Box.
