Hexominos – Die Spielsteine
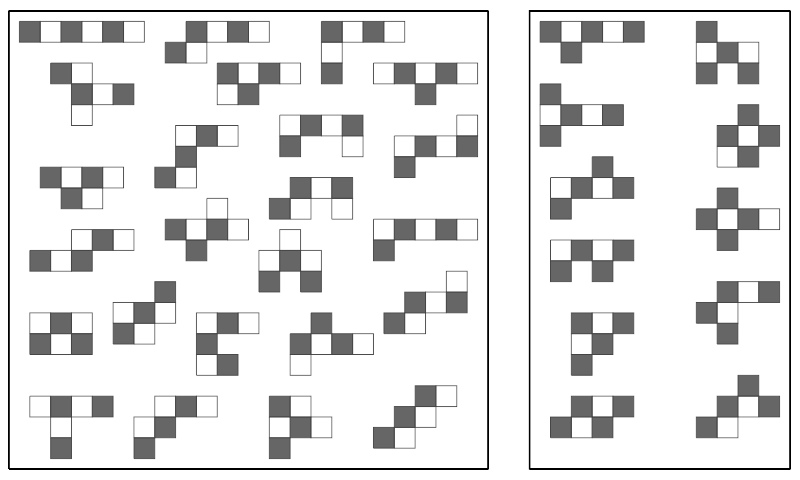
Jedes der 35 Hexominos besteht aus 6 Quadraten. Sie gehören zur Familie der Polyominos.
Verwendet man statt der Quadrate Würfel, lassen sich wie bei den bekannteren Pentominos dreidimensionale Körper konstruieren.

Puzzles aus Hexominos



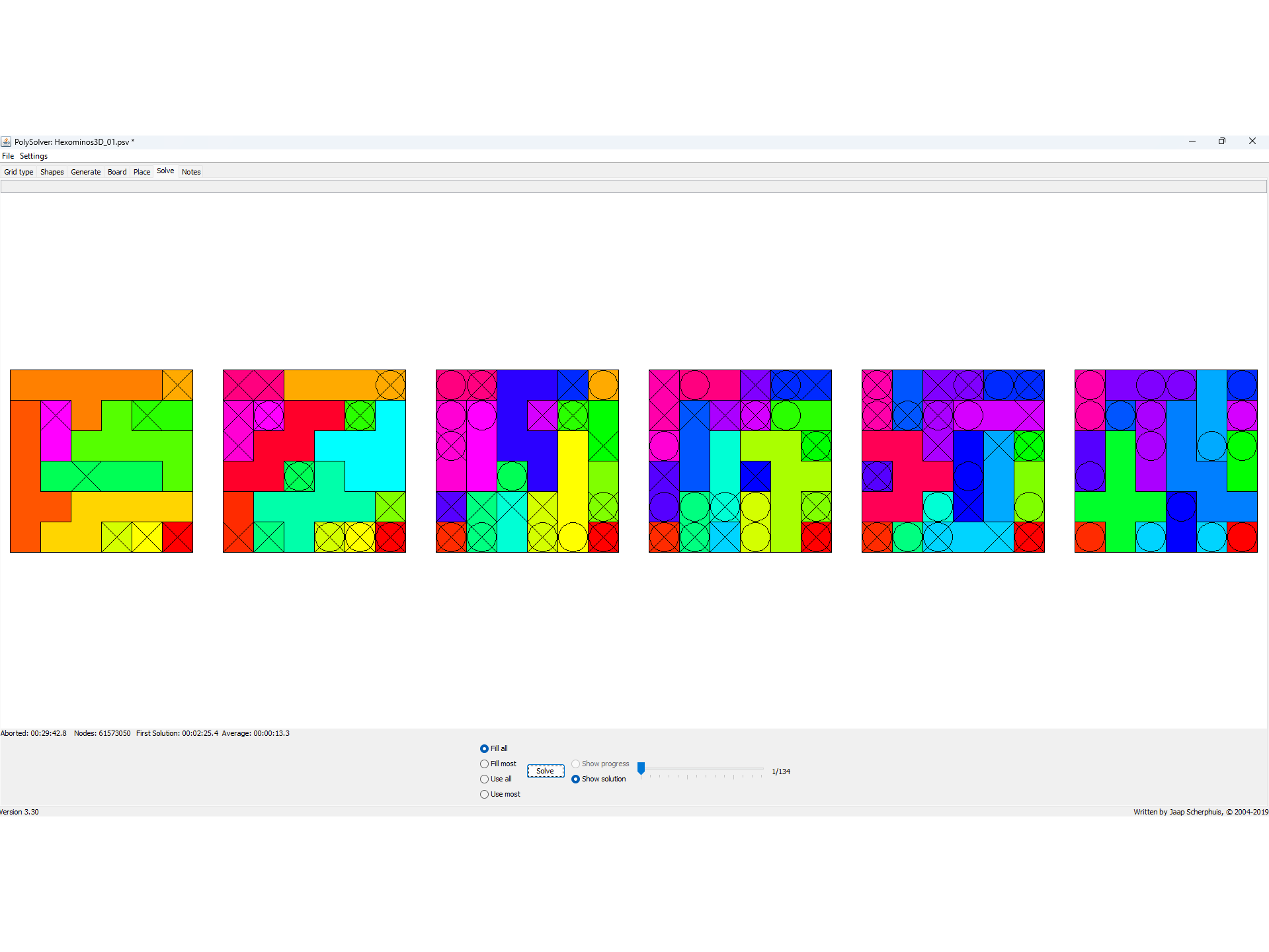
Die 3D-Druck-Vorlagen beinhalten 3 Puzzles. Sie bestehen aus 6, 10 bzw. 36 (ein Hexomino wird doppelt ausgedruckt) Hexominos.
Die Puzzles wurden mit Hilfe des Programms PolySolver gelöst.
Einige Figuren aus Hexominos








Rechtecke aus Hexominos
Eine vollständige Figurensammlung aus 35 Hexominos ergibt eine Fläche von 210 Quadraten. Man könnte erwarten, dass sich damit verschiedene Rechtecke ohne Lücken (sogenannte kompakte Rechtecke) legen lassen. Dass dies jedoch nicht möglich ist, zeigt sich am Beispiel eines Rechtecks mit den Maßen 21 × 10.
Färbt man alle 35 Hexominos im Schachbrettmuster ein (siehe rechtes Bild), lassen sich zwei Arten von Spielsteinen unterscheiden:
- 24 ungerade Hexominos, die jeweils aus genau 3 schwarzen und 3 weißen Feldern bestehen.
- 11 gerade Hexominos, bei denen die Farbverteilung 4 : 2 oder 2 : 4 beträgt.
Die ungeraden Hexominos ergeben in Summe 72 schwarze und 72 weiße Quadrate. Auch bei den geraden Hexominos ergibt sich insgesamt eine gerade Anzahl schwarzer und weißer Felder. Die 35 Hexominosteine enthält also jeweils eine gerade Anzahl schwarzer und weißer Felder.
Färbt man nun das 21 × 10-Rechteck ebenfalls im Schachbrettmuster ein (siehe rechtes Bild), erhält man 105 schwarze und 105 weiße Felder – jeweils eine ungerade Zahl.
Da sich eine gerade Anzahl an schwarzen und weißen Feldern (aus den Hexominos) nicht auf ein Feldmuster mit ungerader Anzahl schwarzer und weißer Felder abbilden lässt, ist eine lückenlose Belegung des Rechtecks unmöglich.
Da dieses Paritätsargument für alle Rechtecke mit 210 Feldern gilt, existiert kein kompaktes Rechteck, das sich vollständig mit allen 35 Hexominos füllen lässt.

Ressourcen & Downloads
3D-Druck-Vorlagen
3D-Druckvorlagen für 3 Puzzles
Als Grundbausteine verwenden die 3D gedruckten Hexominos Würfel anstelle von Quadraten. Man kann sie auch als eine Auswahl von Hexakuben betrachten, so dass auch 3‑dimensionale Figuren gebaut werden können.