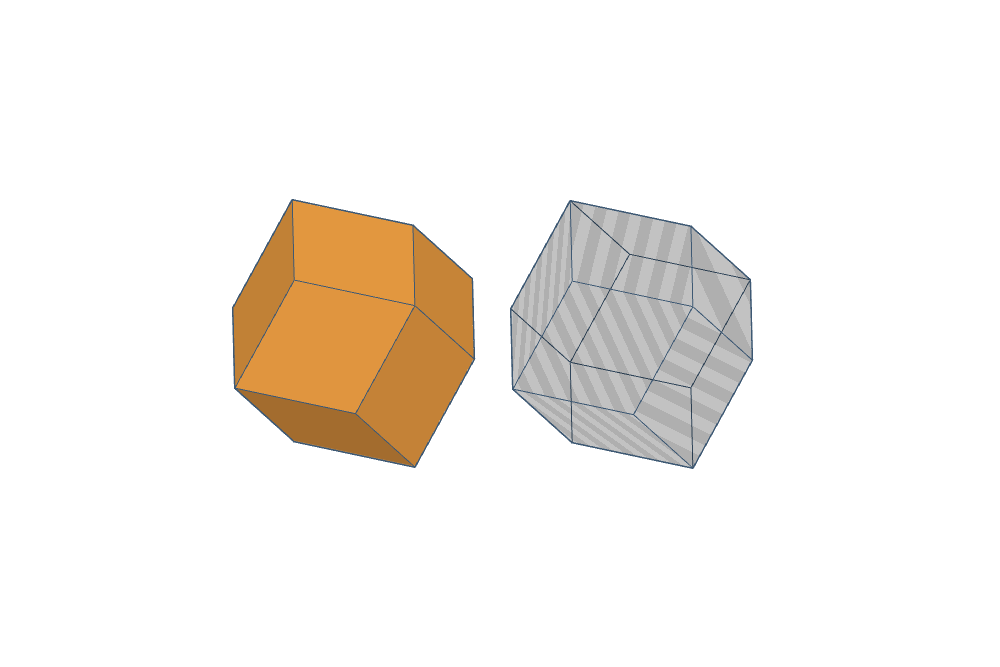
The basic shape of the polyrhons is the rhombic dodecahedron. Rhombic dodecahedra have twelve rhombus-shaped faces, 14 vertices, and 24 edges. When several rhombic dodecahedra are joined face to face, they form polyrhombic dodecahedra – or, in short, polyrhons.

Polyrhons fill space without gaps.

There is 1 dirhon, 5 trirhons, 28 tetrarhons, 225 pentarhons, and 2,274 hexarhons.

Selection of game pieces

Since 5 trirhones are a bit too few for a puzzle and 28 tetrarhones are rather many, the 14 flat tetrarhones are well suited as a basis for a 3D puzzle.
They can be used to build cuboids and several other 3D shapes; tetrahedra and pyramids are the most stable among them.

Fourteen tetrarhones consist of 14×4 = 56 units. This matches exactly the number required for a tetrahedron with edge length 6.
For other shapes and sizes, additional trirhones must be used.

Challenges in building shapes

In addition to the lack of stability of many shapes, there is another challenge when assembling real 3D structures:
Many solutions may be theoretically feasible but cannot be built in practice because pieces get stuck or interlock in ways that prevent assembly.

Some Tetrarhones are so similar in appearance that they are difficult to tell apart.
For this reason, the 3D-printing templates offered here include two versions: one without and one with an engraved number.
When reconstructing the shapes using the solution diagrams provided below, it is advisable to use the numbered pieces.

Three Assembly Options

Polyrhones consist of multiple rhombic dodecahedra joined face-to-face. There are several ways to assemble these pieces into stable shapes, depending on which face or vertex of the polyhedron rests on the working surface.

1. Vertices with three edges facing downward
   In this configuration, the piece rests on a vertex where three edges meet. Suitable platforms are Type 1 and Type 2.
   Result: Tetrahedra
   Difference between Type 1 and Type 2: With Type 1, the edge length decreases by 1 per layer; with Type 2, it decreases by 2 per layer.
2. Rhombic faces facing downward
   Here, a rhombic face lies flat on the working surface. Suitable platforms are Type 3.
   Result: Pyramids with rectangular bases.
3. Vertices with four edges facing downward
   In this case, the piece rests on a vertex where four edges meet. Suitable platforms are Type 4.
   Result: Square pyramids.

Type 1 – Tetrahedra with layer reduction of 1

Using the platforms rhontetrabase_4_1, rhontetrabase_5_1, and rhontetrabase_6_1, you can build tetrahedra with edge lengths of 4, 5, and 6, respectively.

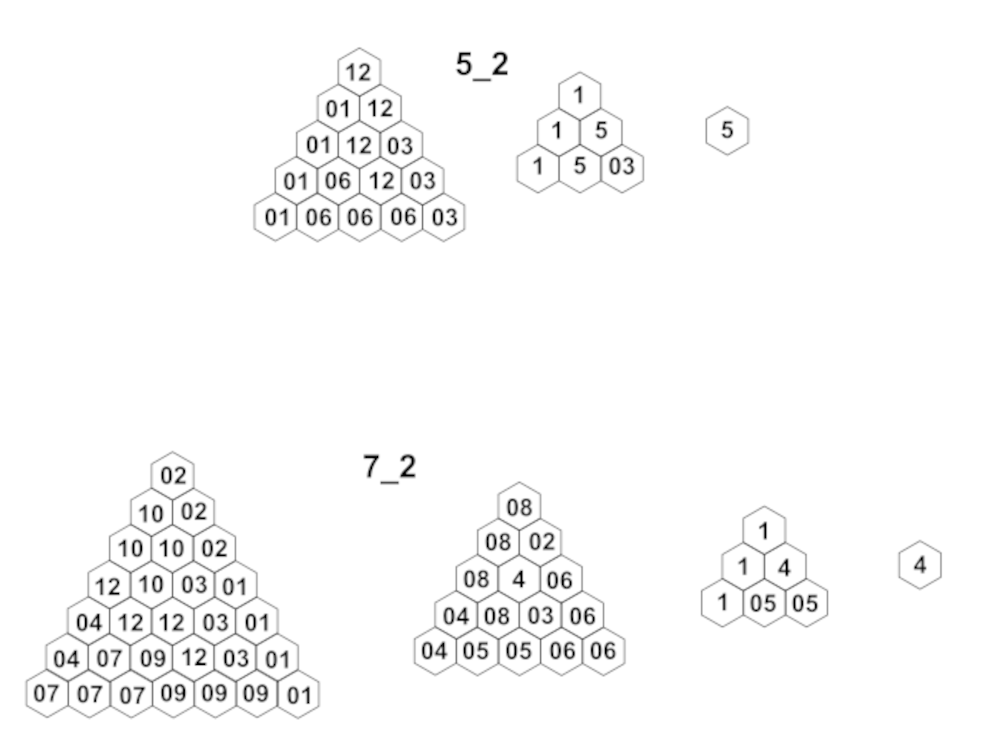
Type 2 – Tetrahedra with layer reduction of 2

Using the platforms rhontetrabase_5_2 und rhontetrabase_7_2 you can build also tetrahedra.

• Basis rhontetrabase_5_2: drei Schichten (Kantenlängen 5, 3, 1)
• Basis rhontetrabase_7_2: vier Schichten (Kantenlängen 7, 5, 3, 1)

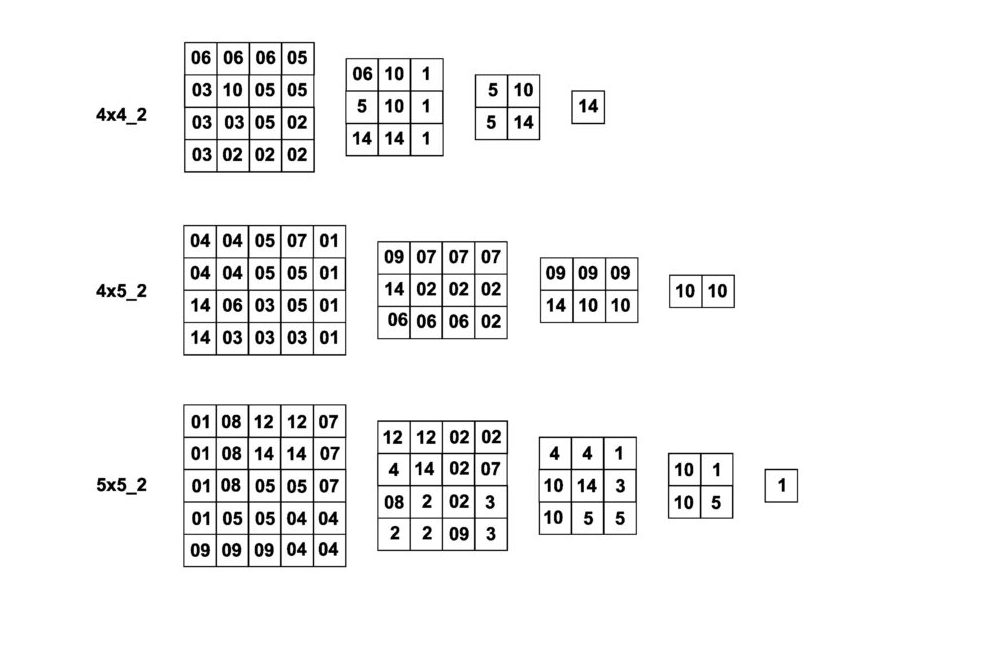
Type 3 – Pyramids with a Rectangular Base

Here the rhombi lie on the bottom.
Using rhonpyrabase_4_1 and rhonpyrabase_5_1, you can build pyramids with edge lengths 4 and 5, respectively.
With rhonpyrabase_5x4, you can construct a 5×4 roof.

Type 4 – Square pyramids

Here, vertices with four edges are placed on the bottom.
Using the platforms rhonpyrabase_4_2 and rhonpyrabase_5_2, you can build pyramids with edge lengths of 4 and 5, respectively.
With rhonpyrabase_5x4_2, you can construct a 5×4 roof.

The 3D-print files consist of 11 platforms, 5 trirhones, and 14 tetrarhones.