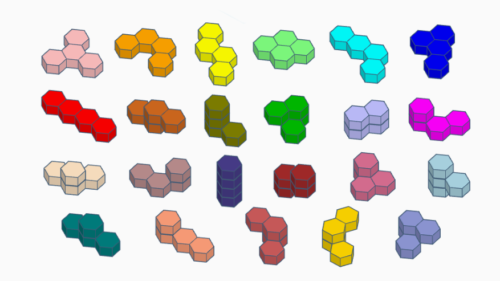
HexaPrisma — Spielsteine
Das HexaPrisma Puzzle gehört zur Familie der Polyhexprismen. Jeder der 23 Spielsteine besteht aus 4 regulären Sechseckprismen (Tetrahexprismen).
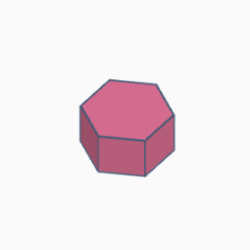
Durch Extrusion eines regelmäßigen Sechsecks erhält man ein reguläres Sechseckprisma (siehe auch Wikipedia). Durch Verbinden mehrerer solcher Prismen erhält man Polyhexprismen oder gestapelte Polyhexen (“stacked polyhexes”).
Puzzles aus Tetrahex-Prismen
Es ist naheliegend aus den 23 Tetrahex-Prismen eine Figur mit 4 gleichen Schichten zu erstellen, wobei jede Schicht aus 23 Sechsecken besteht (Abbildung 1). Dies ist jedoch aus folgendem Grund nicht möglich:
Wir betrachten dazu die Summe der Hexagone der ungeraden, also der 1. und 3. Schicht. Sie beträgt 46 (eine gerade Zahl).
Schaut man sich jetzt die einzelnen Tetrahexprismen an, so gilt für 16 der 23 Spielsteine:
für eine beliebige Positionen in der Figur beträgt die Anzahl der Sechsecke in den ungeraden Schichten 0, 2 oder 4. Die Summe der Sechsecke dieser 16 Spielsteine in den ungeraden Schichten ist damit gerade (“16 x gerade = gerade”).
Für 7 Spielsteine gilt, dass die Anzahl ihrer Sechsecke in den ungeraden Schichten 1 oder 3 beträgt. Addiert man die Hexagons der 7 Spielsteine in den ungeraden Schichten erhält man eine ungerade Zahl (“7 x ungerade = ungerade”).
Insgesamt folgt daraus, dass die Summe der Sechsecke aller Tetrahexprismen in den ungeraden Schichten immer ungerade ist (“gerade + ungerade = ungerade”).
Allgemein gilt: damit eine Figur, bestehend aus allen Tetrahexprismen lösbar ist, muss die Summe der Sechsecke in den ungeraden Schichten ungerade sein. Die Anzahl der Sechsecke in den geraden Schichten muss ebenfalls ungerade sein.
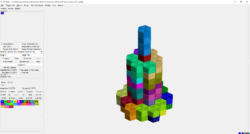
Die symmetrische Figur in Abbildung 2 erfüllt diese Voraussetzung. Sie besteht aus 49 Sechsecken in den ungeraden und 43 Sechsecken in den geraden Schichten. Die Figur stammt von der Webseite polyforms.eu.
Die auf dieser Webseite angebotenen 3D-Druckvorlagen für Tetrahexpuzzles bestehen aus 4 gleichen Schichten und bestehen deshalb aus weniger als 23 Tetrahexprismen.
Die Lösungen wurden mit dem Programm Burr Tools berechnet.
Lösungsvideo