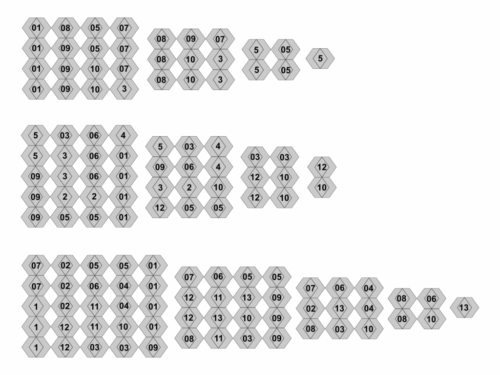Polyrhone

Da 5 Trirhone für ein Puz­zle etwas wenig und 28 Tetrarhone ziem­lich viel sind, bieten sich die 14 flachen Tetrarhone als Basis für ein 3D-Puz­zle an. Es lassen sich Quad­er und einige andere 3D-For­men bauen, Tetraed­er und Pyra­mi­den sind davon die sta­bil­sten. 14 Tetrarhone beste­hen aus 4 x 14 = 56 Ein­heit­en. Das passt genau, für ein Tetraed­er der Kan­ten­länge 6. Für andere For­men und Größen muss man die Trirhone zur Hil­fe nehmen.

Neben der man­gel­nden Sta­bil­ität viel­er For­men gibt es ein weit­eres Prob­lem beim Zusam­men­bau “real­er 3D-Fig­uren”: Viele Lösun­gen sind zwar the­o­retisch möglich, aber beim Zusam­men­fü­gen klem­men die Spiel­steine oder sind so umeinan­dergewick­elt, dass sie sich gar nicht zusam­men­bauen lassen.

Manche der Tetrarhone sind sich so ähn­lich, dass sie nur schw­er zu unter­schei­den sind. Deshalb gibt es für die hier zum Down­load ange­bote­nen 3D-Druck­vor­la­gen der Spiel­steine jew­eils 2 Vari­anten: eine ohne und eine mit “ein­graviert­er” Num­mer. Um die Fig­uren nach den unten angegebe­nen Lösungsvor­la­gen nachzubauen, ist es empfehlenswert, die num­merierten Spiel­steine zu ver­wen­den.

Für die Fig­uren ste­hen 11 Plat­tfor­men zum Down­load bere­it. Es gibt es 4 ver­schiedene Arten von Plat­tfor­men, abhängig davon, welche Fläche, Kante bzw. Ecke der Polyrhone unten liegt. Für einige 3D-For­men habe ich noch keine Lösun­gen.

Typ 1:

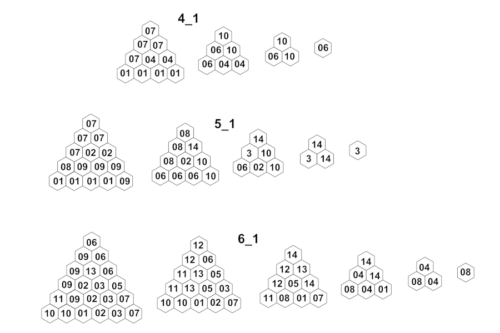
Mit den Plat­tfor­men rhontetrabase_4_1, rhontetrabase_5_1 und rhontetrabase_6_1 baut man Tetraed­er der Kan­ten­länge 4, 5 bzw. 6.

Die in der Grafik angezeigten Lösun­gen ver­wen­den für:

• den Tetraed­er mit Kan­ten­länge 4 die Tetrarhone: 01, 04, 06, 07 und 14.
• den Tetraed­er mit Kan­ten­länge 5 die Tetrarhone: 01, 02, 06, 07, 08, 09, 10 und 14, sowie das Trirhon 3.
• den Tetraed­er mit Kan­ten­länge 6 alle 14 Tetrarhone. Die Lösung für den Tetraed­er mit Kan­ten­länge 6 stammt von der Web­seite polyforms.eu. Selb­st mit Lösungsvor­lage ist dieser Tetraed­er nicht ein­fach zusam­men­zubauen, zumal die Spiel­steine 03 und 05 klem­men.

Typ 2:

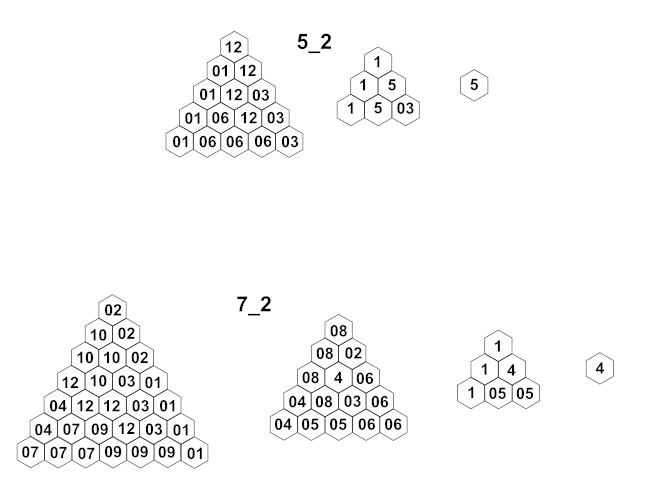
Mit den Plat­tfor­men rhontetrabase_5_2 und rhontetrabase_7_2 baut man eben­falls Tetraed­er (mit Kan­ten­länge 5 bzw. 7). Allerd­ings nimmt die Kan­ten­länge pro Schicht nicht wie beim Typ1-Tetraed­er um 1, son­dern um 2 ab.

• Der Tetraed­er der Basis rhontetrabase_5_2 beste­ht aus nur 3 Schicht­en mit den Kan­ten­län­gen 5, 3 und 1. Die Lösung der Vor­lage ver­wen­det die Tetrarhone 01, 03, 06 und 12 und die Trirhone 1 und 5.
• Der Tetraed­er der Plat­tform rhontetrabase_7_2 hat 4 Schicht­en der Kan­ten­län­gen 7, 5, 3 und 1. Eine Lösung für den Tetraed­er mit Kan­ten­länge 7 habe ich (noch) nicht gefun­den.

Typ 3:

Bei diesem Typ liegen die Raut­en der Polyrhone unten. Mit den Plat­tfor­men rhonpyrabase_4_1 und rhonpyrabase_5_1 baut man Pyra­mi­den mit Kan­ten­länge 4 bzw. 5. Die Grund­flächen der Pyra­mi­den sind nicht qua­dratisch. Mit der Plat­tform rhonpyrabase_5x4 erhält man ein 5x4-Dach.

Für die Pyra­mide der Plat­tform rhonpyrabase_4_1 wer­den die Tetrarhone 01, 05, 07, 08, 09 und 10, sowie die Trirhone 3 und 5 ver­wen­det. Für die Pyra­mide mit Kan­ten­länge 5 und für das 5x4-Dach habe ich noch keine Lösun­gen.

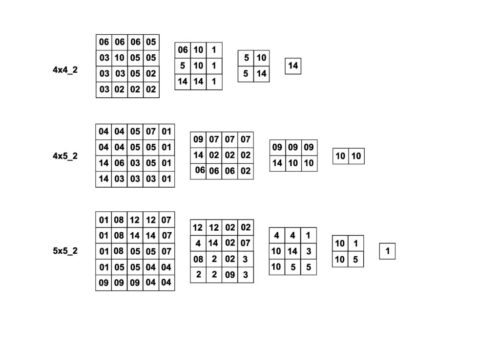
Typ 4:

Mit den Plat­tfor­men rhonpyrabase_4_2 und rhonpyrabase_5_2 baut man eine Pyra­mide mit Kan­ten­länge 4 bzw 5. Mit der Plat­tform rhonpyrabase_5x4_2 baut man ein 5x4-Dach.

• die Lösungsvor­lage für die Pyra­mide mit Kan­ten­länge 4 enthält die Tetrarhone: 02, 03, 05, 06, 10 und 14 und die Trirhone 1 und 5.
• die Lösungsvor­lage für das 5x4-Dach enthält die Tetrarhone: 01, 02, 03, 04, 05, 06, 07, 09, 10 und 14.
• für die 5x5-Pyra­mide habe ich noch keine Lösung gefun­den.