Tetracairo – Die Spielsteine
Tetracairo – ein Puzzle auf Basis eines Fünfecks
Die Tetracairos gehören zur Familie der Polycairos. Sie bestehen aus Fünfecken mit 2 rechten Innenwinkeln. Diese Fünfecke eignen sich zur Parkettierung, sie überdecken die Fläche also lückenlos und überlappungsfrei.
Es gibt 2 Dicairos, 5 Tricairos, 17 Tetracairos, 55 Pentacairos, 206 Hexacairos, 781 Heptacairos und 3099 Octacairos.

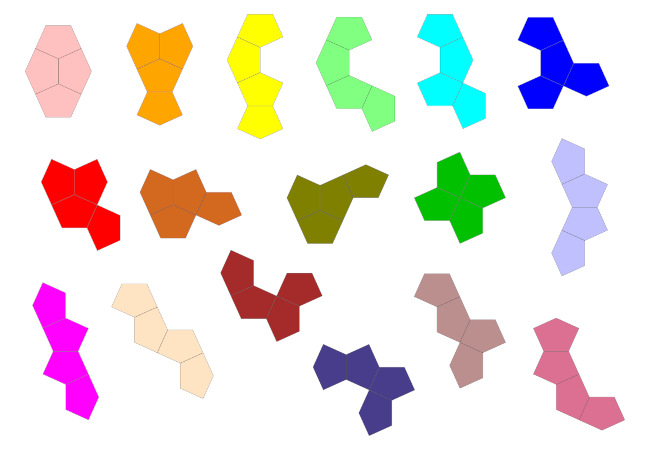

Tetracairo-Puzzles
Warum es keine spiegelsymmetrische Figur aus allen 17 Tetracairos gibt
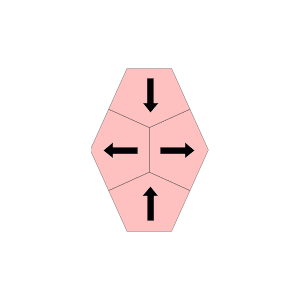
Innerhalb des Gitters lassen sich alle Tetracairo-Spielsteine um 90° drehen. Dabei zeigen die Spitzen der Fünfecke eines Spielsteins entweder in horizontale oder in vertikale Richtung.
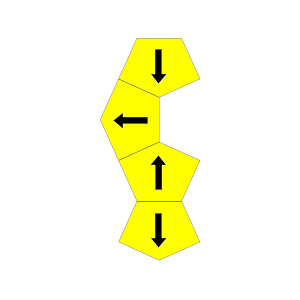
Bei 12 der 17 Tetracairos zeigt – unabhängig von der Drehung – jeweils die Hälfte der Fünfecke in horizontale und die andere Hälfte in vertikale Richtung. Bei den übrigen 5 Tetracairos ist die Verteilung asymmetrisch: Drei Fünfecke zeigen in die eine, nur eines in die andere Richtung (entweder 3:1 oder 1:3).
Wenn man eine Figur aus allen 17 Tetracairos zusammensetzt, ergibt sich daraus eine Differenz von 2, 6 oder 10 zwischen der Anzahl horizontal und vertikal ausgerichteter Fünfecke.
Eine spiegelsymmetrische Figur müsste jedoch eine gleichmäßige Verteilung aufweisen – also eine Differenz von 0, 4, 8 usw. Da diese Bedingung nicht erfüllt ist, kann keine spiegelsymmetrische Figur aus allen 17 Tetracairos existieren.
Aus 16 oder weniger Tetracairo-Spielsteinen lassen sich viele symmetrische Formen bilden.
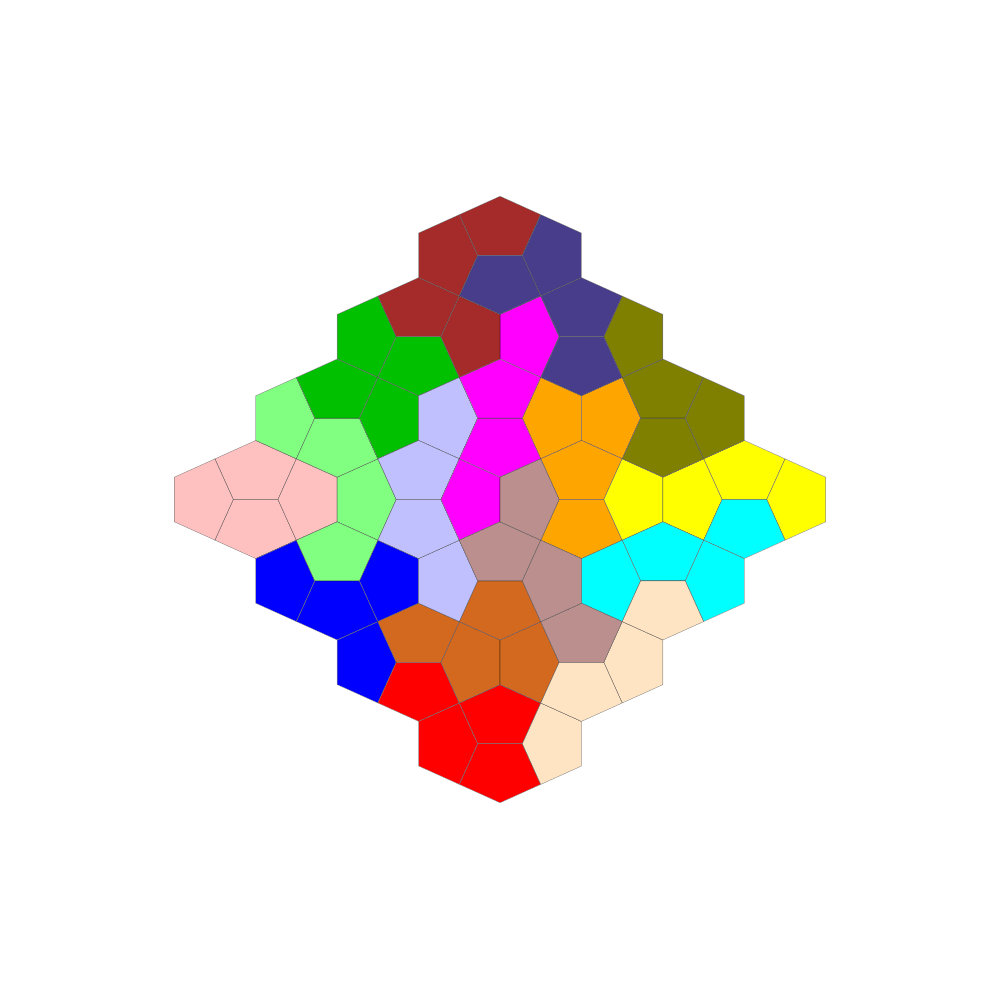


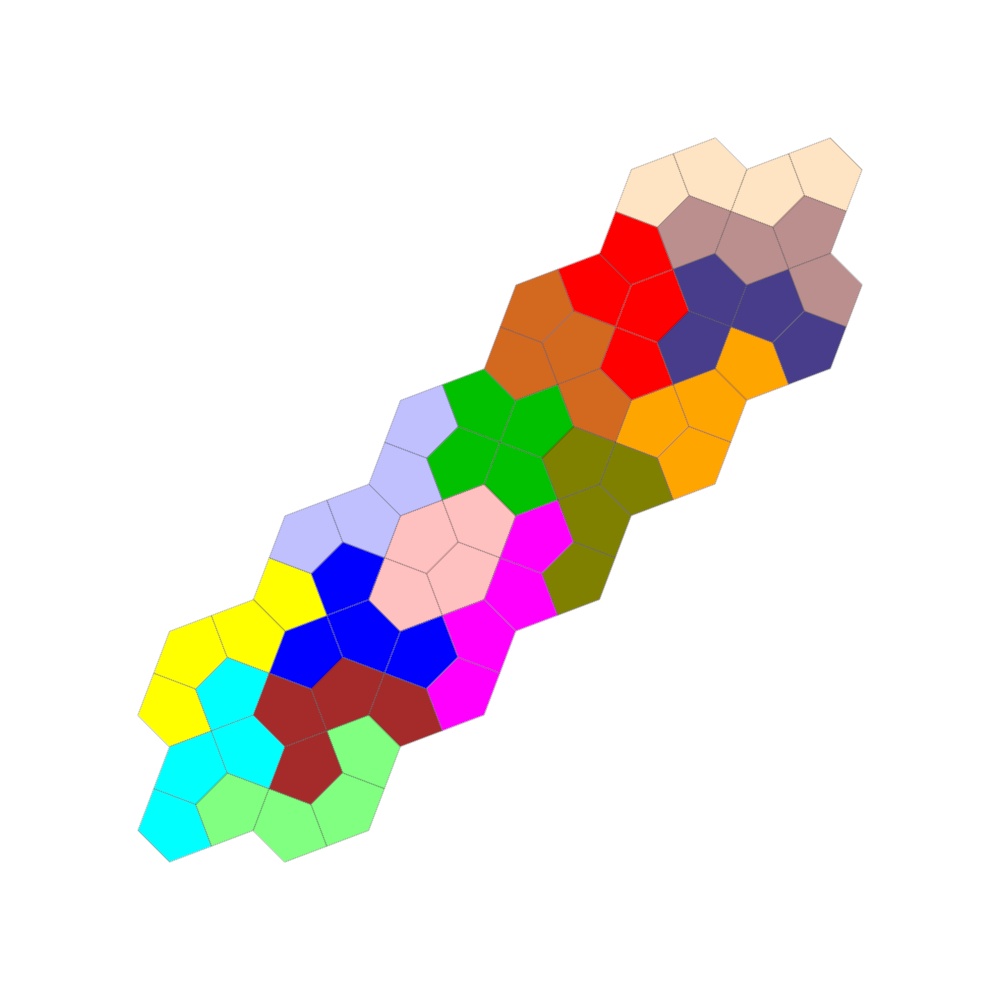
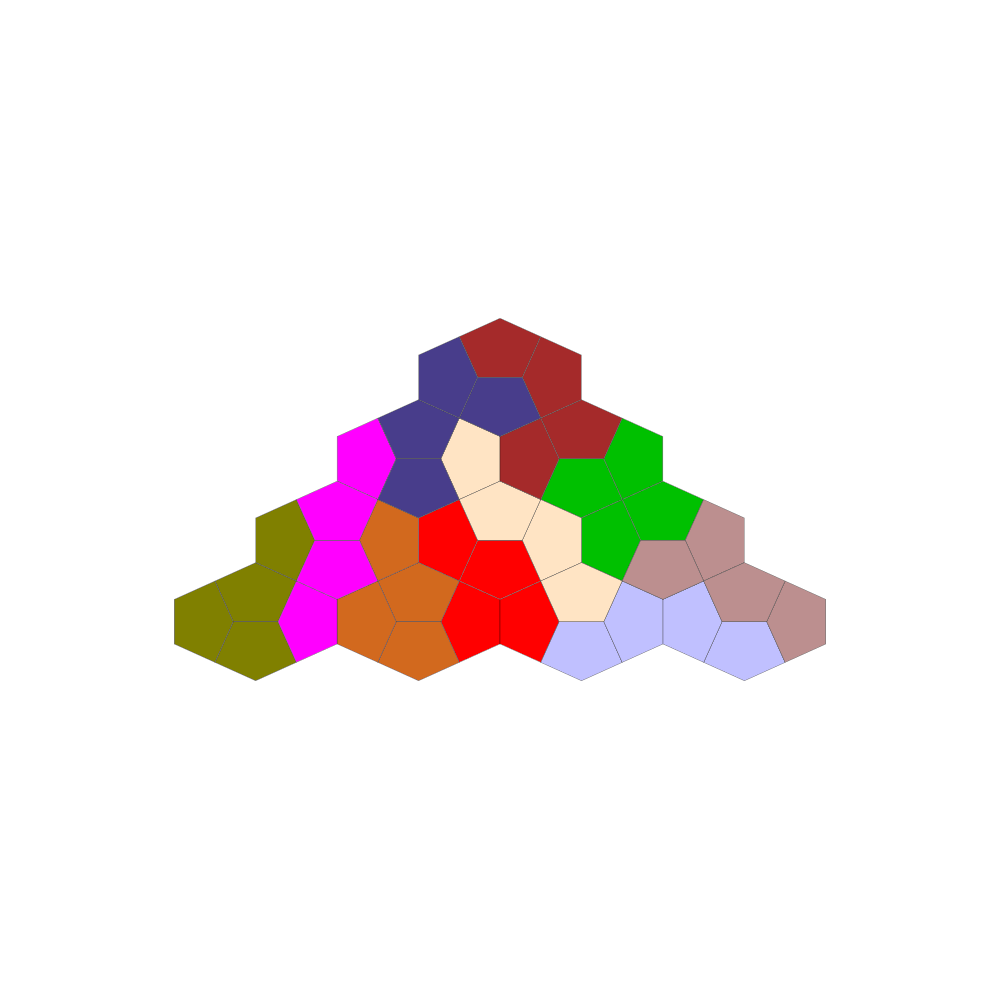



Ressourcen & Downloads
3D-Druck-Vorlagen
Die 3D-Druckvorlagen bestehen aus den 17 Tetracairos und einer Box.


Online Lösungsprogramm
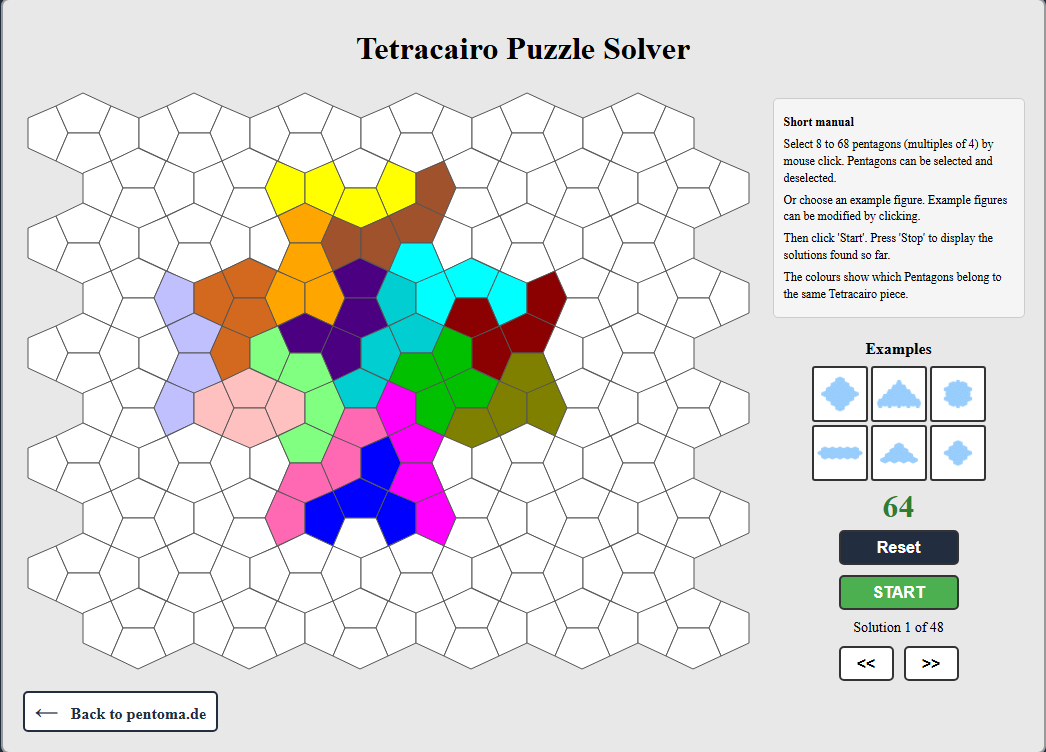
Der Online-Tetracairo-Solver läuft direkt im Browser – ohne Installation und ohne Download. Figuren lassen sich einfach per Mausklick zusammenstellen und anschließend berechnen.
Neben Figuren aus allen 17 Tetracairosteinen können auch Lösungen von Formen, die aus 2 bis 16 Steinen bestehen, berechnet werden.
Die gefundenen Lösungen werden ohne Symmetriebereinigung ausgegeben – Lösungen, die durch Drehung oder Spiegelung ineinander überführt werden können, werden als separate Lösungen gezählt. Für einige wenige Figuren benötigt das Programm etwas länger (einige Minuten), um die erste Lösung zu finden.
Das Programm ist auf Englisch, die Bedienung ist jedoch einfach und sehr intuitiv.
Lösungsprogramm

In der Programmsammlung, die auf itch.io zum Herunterladen bereitsteht, ist ein Lösungsprogramm zum Erstellen und Lösen von Tetracairofiguren enthalten. Es läuft ausschließlich unter Windows.
WICHTIG: Für eine fehlerfreie Installation bitte vor dem Entpacken die Hinweise beachten!