Tetracairo — Spielsteine
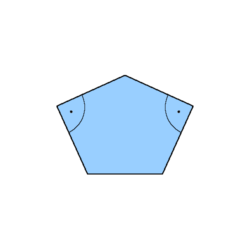
Die Tetracairos gehören zur Familie der Polycairos. Die Grundform der Polycairos ist ein Fünfeck mit zwei rechten Innenwinkeln. Diese Fünfecke eignen sich zur Parkettierung (sie überdecken die Ebene also lückenlos und überlappungsfrei).
Puzzles aus Tetracairos
Es gibt keine spiegelsymmetrischen Figuren, die aus allen 17 Tetracairos bestehen. Der Grund dafür ist folgender:
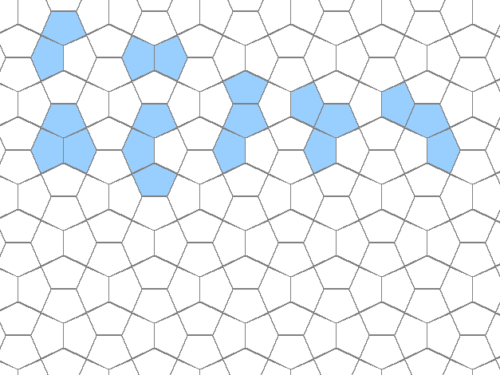
Innerhalb des Gitters lässt sich jeder Tetracairo-Spielstein um 90° drehen. Dabei zeigen die Spitzen der Fünfecke eines Spielsteines entweder in horizontaler oder vertikaler Richtung.
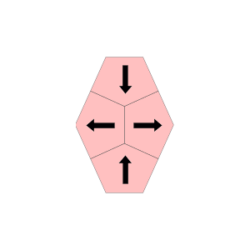
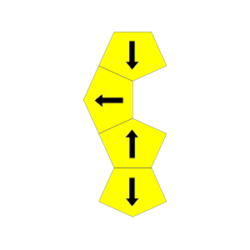
Bei 12 der 17 Tetracairos zeigen jeweils 2 der Fünfecke in horizontaler und 2 in vertikaler Richtung, egal wie man sie innerhalb des Gitters dreht. Bei den restlichen 5 Tetracairos zeigen immer 3 Fünfecke in horizontaler und 1 Fünfeck in vertikaler Richtung bzw. 3 Fünfecke in vertikaler und 1 Fünfeck in horizontaler Richtung.
Bei Figuren, die aus allen 17 Tetracairos bestehen, ist die Differenz zwischen horizontal und vertikal ausgerichteten Fünfecken also 2 oder 6 oder 10.
Für spiegelsymmetrische Figuren, die aus 68 Fünfecken (17 Tetracairos aus je 4 Fünfecken) bestehen, müsste die Differenz zwischen horizontal und vertikal ausgerichteten Fünfecken aber 0 oder 4 oder 8 etc. betragen.
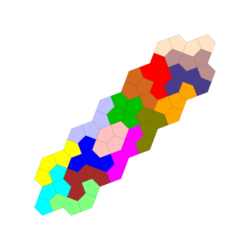
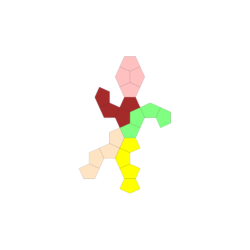
Aus 16 oder weniger Tetracairo-Spielsteinen lassen sich viele symmetrische Formen bilden.
Die folgenden Figuren stammen von den Teilnehmern der Mathechallenge Oberfanken unter der Leitung von Erik Sinne
Was findet man auf dieser Webseite?
- ein Lösungsprogramm für Tetracairo-Figuren
- 3D-Druckvorlagen für ein Tetracairo-Puzzle
- eine kurze Beschreibung der Polycairos
externe Links