Tetrahexe – Pentoma Puzzles

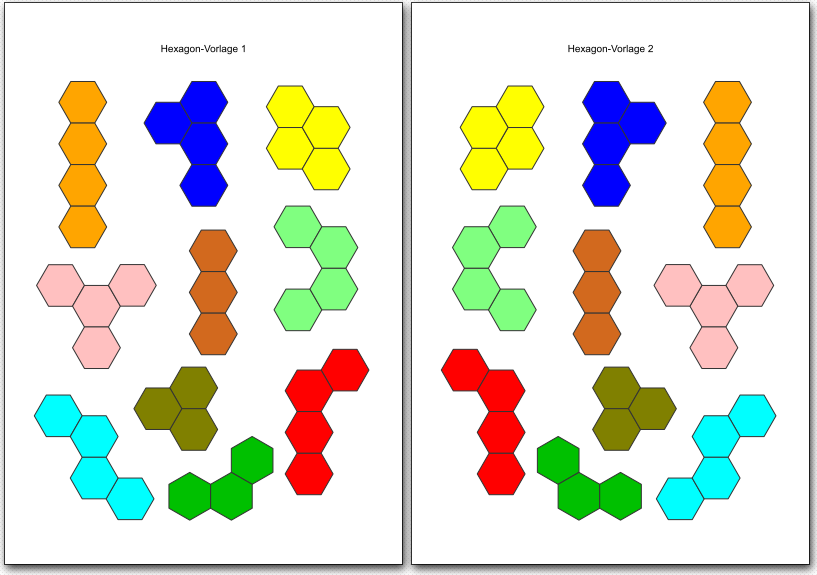
Tri- und Tetrahex – Spielsteine

Durch Zusammenfügen von 3 regelmäßigen Sechsecken erhält man Trihexe. Die Tetrahexe bestehen aus 4 verbundenen Hexagonen.

Es gibt 3 Tri- und 7 Tetrahexe. Sie gehören zur Familie der Polyhexe.

3 Trihexe und 7 Tetrahexe — alle Tri- und Tetrahexe

Puzzles aus Tri- und Tetrahexen

Es gibt genau drei regelmäßige Vielecke – also Figuren mit gleich langen Seiten und gleichen Innenwinkeln –, mit denen sich eine Fläche lückenlos parkettieren lässt: das Quadrat, das gleichseitige Dreieck und das regelmäßige Sechseck.

So wie aus dem Quadrat die Pentominos und aus dem gleichseitigen Dreieck die Hexiamonds entstanden sind, lag es nahe, auch aus regelmäßigen Sechsecken ein passendes Legespiel zu entwickeln: ein Puzzle aus sogenannten Polywaben.

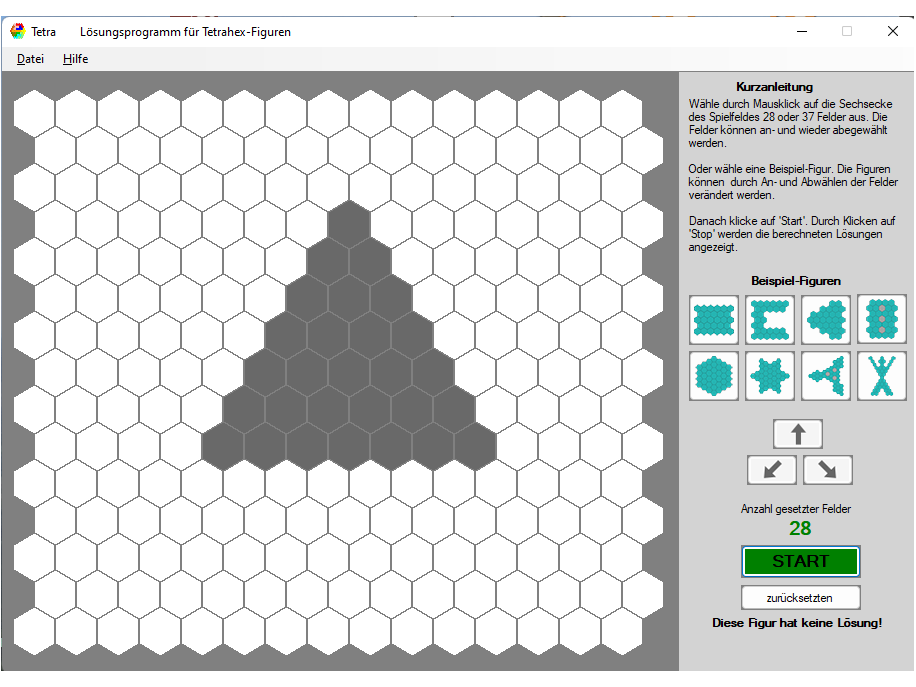
Die 7 Tetrahex-Steine bilden zusammen eine Fläche aus 28 Sechsecken. Ergänzt man sie um die 3 Trihex-Steine, ergibt sich ein vollständiger Satz mit 37 Waben. Auf der Figurenübersichtsseite findet man einige Beispiele für Figuren, die sich mit den Tetrahexen legen lassen.

Das zugrunde liegende Wabengitter erlaubt 6 Spiegelachsen und 6 Drehachsen (also maximale Symmetrie). Wenn man sich auf die 7 Tetrahexen beschränkt, gibt es jedoch keine Figur mit maximaler Symmetrie – selbst ein gleichseitiges Dreieck (wie abgebildet) lässt sich damit nicht legen.

Erweitert man den Satz um die 3 Trihex-Steine, so existieren zwei Figuren mit maximaler Symmetrie: ein Hexagon und eine „Schneeflocke“ – vermutlich sind es auch die einzigen Figuren mit dieser Eigenschaft.