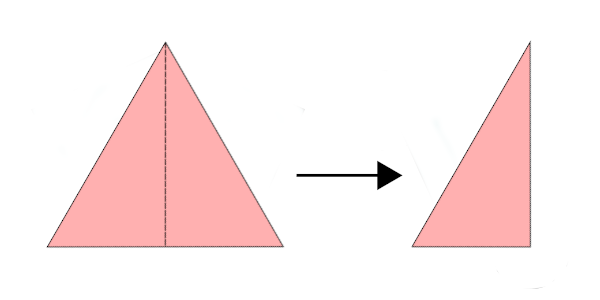
Ein Monodrafter – kurz Drafter – ist ein rechtwinkliges Dreieck mit den Innenwinkeln 30°, 60° und 90°. Aus verbundenen Draftern werden Polydrafter. Die möglichen Sets dieser Polydrafter hängen von dem zugrundeliegenden Gitter ab. Die hier betrachteten Tridrafter fügen sich in das Dreiecksgitter ein.

Beim Bilden von Polyformen wird in der Regel stillschweigend vorausgesetzt, dass sich zwei Grundformen an ihrer vollständigen Seitenlänge verbinden müssen. Da bei einem Drafter die kürzere Kathete nur halb so lang ist wie die Hypotenuse, lässt sich diese Regel erweitern: Auch eine Verbindung über die halbe Hypotenusenlänge wird als gültig angesehen. Diese Erweiterung ermöglicht zusätzliche Verbindungsvarianten – auch bei den hier betrachteten Tridraftern.

Mit diesen beiden Vorgaben ergeben sich 6 Didrafter, 14 Tridrafter, 64 Tetradrafter, 237 Pentadrafter, 1025 Hexadrafter.

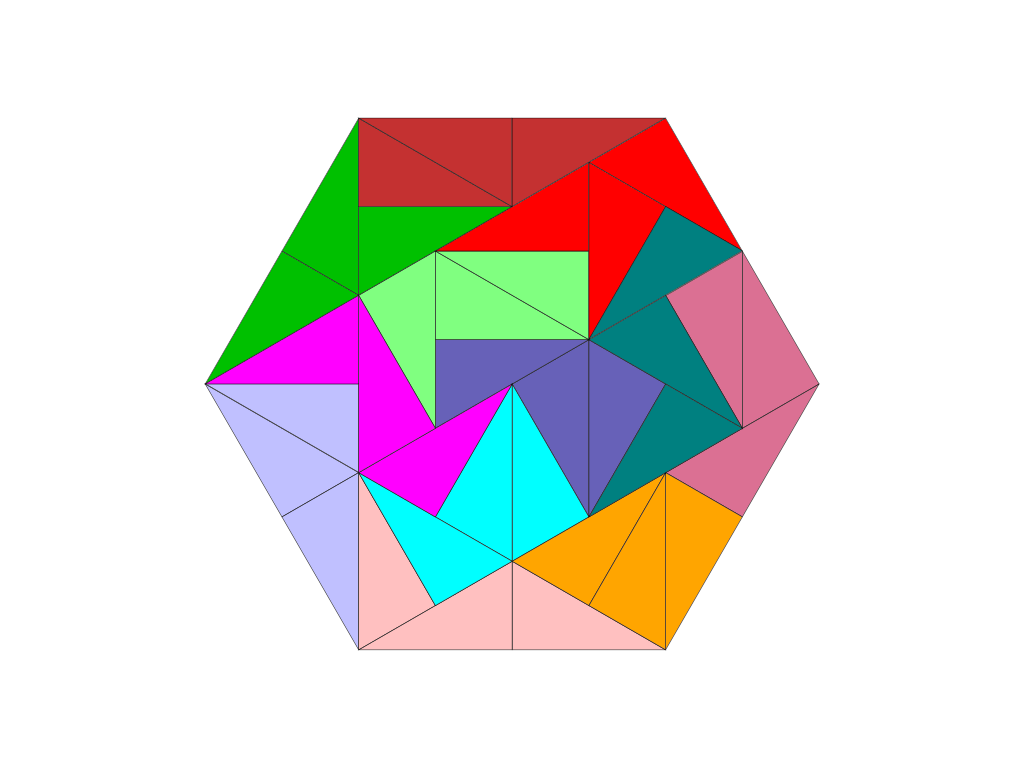
Figuren aus 14 Tridraftern bestehen aus 42 Dreiecken. Das zugrundeliegende Dreiecksgitter erlaubt Figuren mit sechs Spiegelachsen und sechsfacher Drehsymmetrie. Eine Figur mit maximaler Symmetrie, die aus nur 12 Spielsteinen besteht, ist beispielsweise das unten abgebildete Hexagon. Eine Figur mit voller Symmetrie, die alle 14 Tridrafter einbezieht, ist bislang nicht bekannt. Die Figur „Sägeblatt“ weist immerhin eine sechsfach Drehsymmetrie auf.

Gemeinsam ist allen Figuren, die aus den 14 Tridraftern bestehen, dass sie nur wenige mögliche Lösungen haben. Der Schwierigkeitsgrad entsprechender Puzzles ist hoch und bewegt sich – zumindest für einen Menschen – zwischen „sehr schwierig“ und „praktisch unlösbar“.

Weitere Infos zu Tridraftern gibt es auf Logelium.

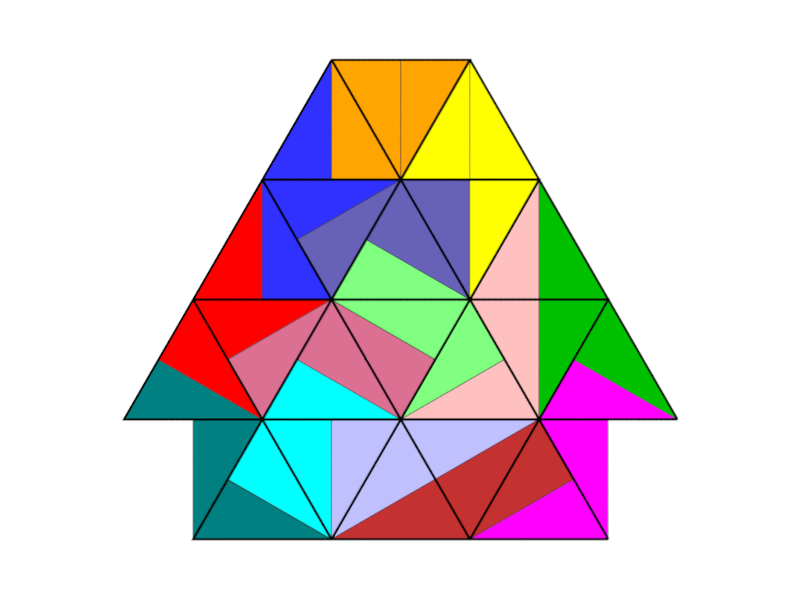
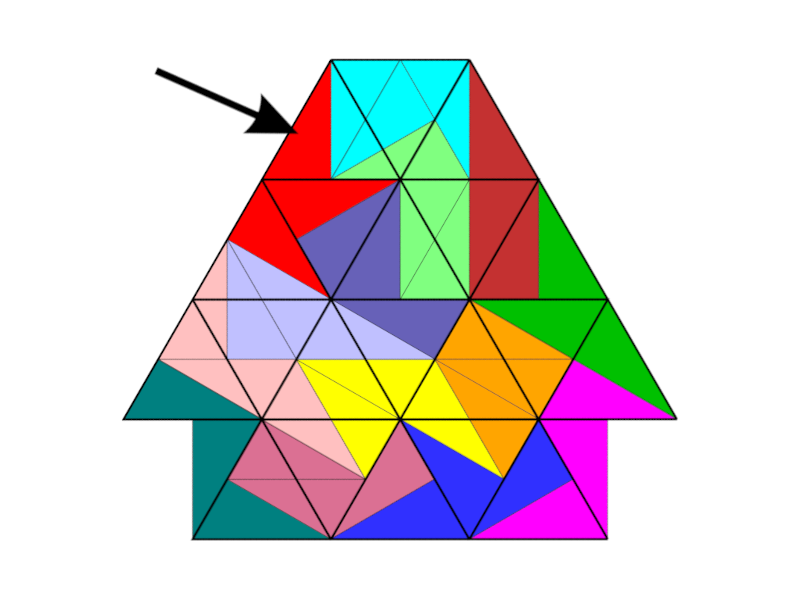
Die 14 Tridrafter fügen sich in ein Gitter aus gleichseitigen Dreiecken ein. Sie verhalten sich damit „gitterkonform“. Für Figuren, die aus diesen Spielsteinen zusammengesetzt werden, trifft dies jedoch nur selten zu. In den meisten Lösungen halten sich die Tridrafter nicht durchgängig an die vorgegebene Gitterstruktur – es kommt zu sogenannten „Gittersprüngen“.

Die beiden Abbildungen zeigen exemplarisch eine gitterkonforme und eine nicht gitterkonforme Figur.

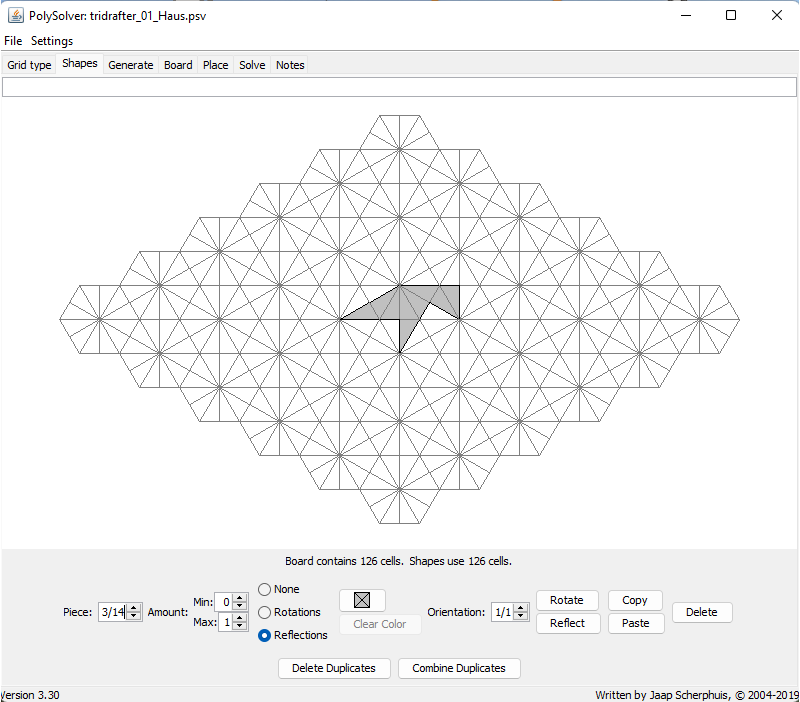
Diese Unterscheidung zwischen gitterkonformen und nicht gitterkonformen Figuren spielt insbesondere beim Einsatz von Lösungssoftware eine Rolle.

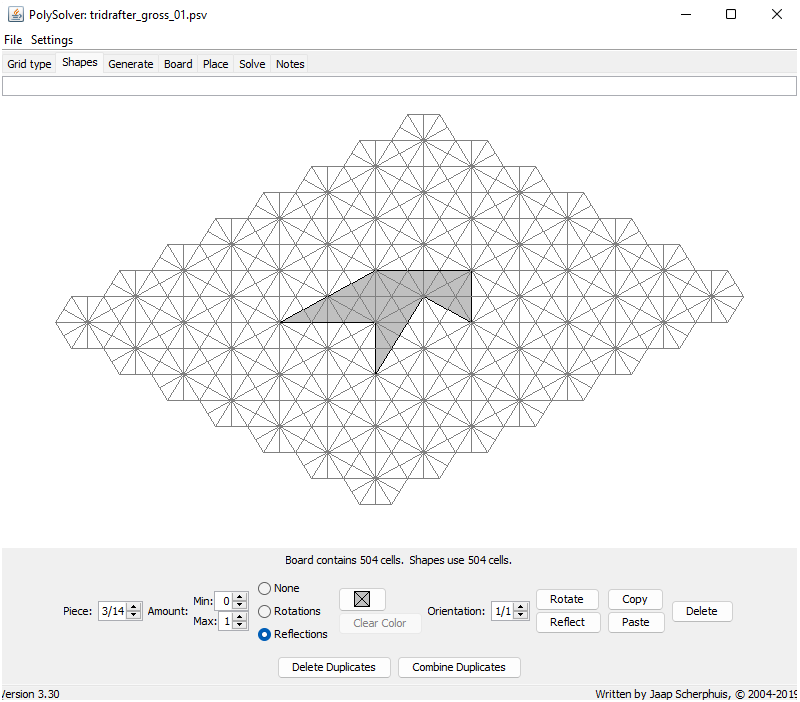
Beim Erstellen der Tridrafter-Spielsteine im Programm PolySolver wirkt sich die Wahl der internen Struktur auf die Art der möglichen Lösungen aus. Werden die Spielsteine jeweils aus 9 Dreiecken aufgebaut (siehe Abbildung 1), entstehen ausschließlich gitterkonforme Lösungen. Verwendet man dagegen 36 Dreiecke pro Spielstein (siehe Abbildung 2), sind auch Lösungen mit Gittersprüngen möglich. Eine Figur, die alle 14 Tridrafter umfasst, besteht bei dieser Darstellung insgesamt aus 504 Dreiecken.

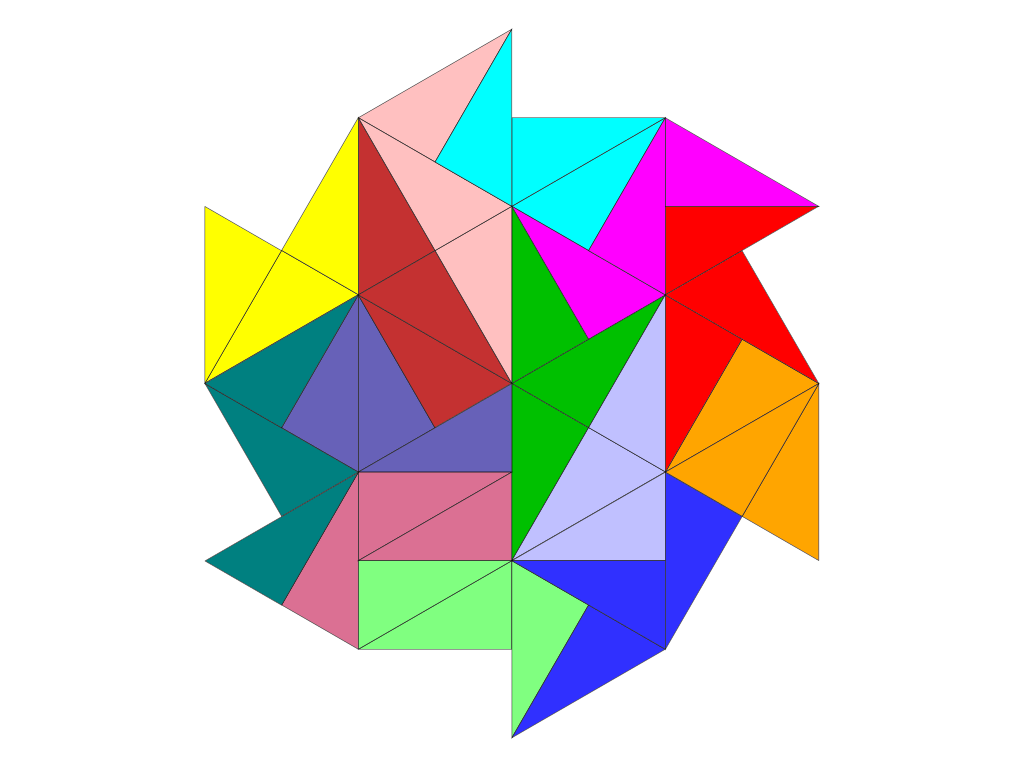
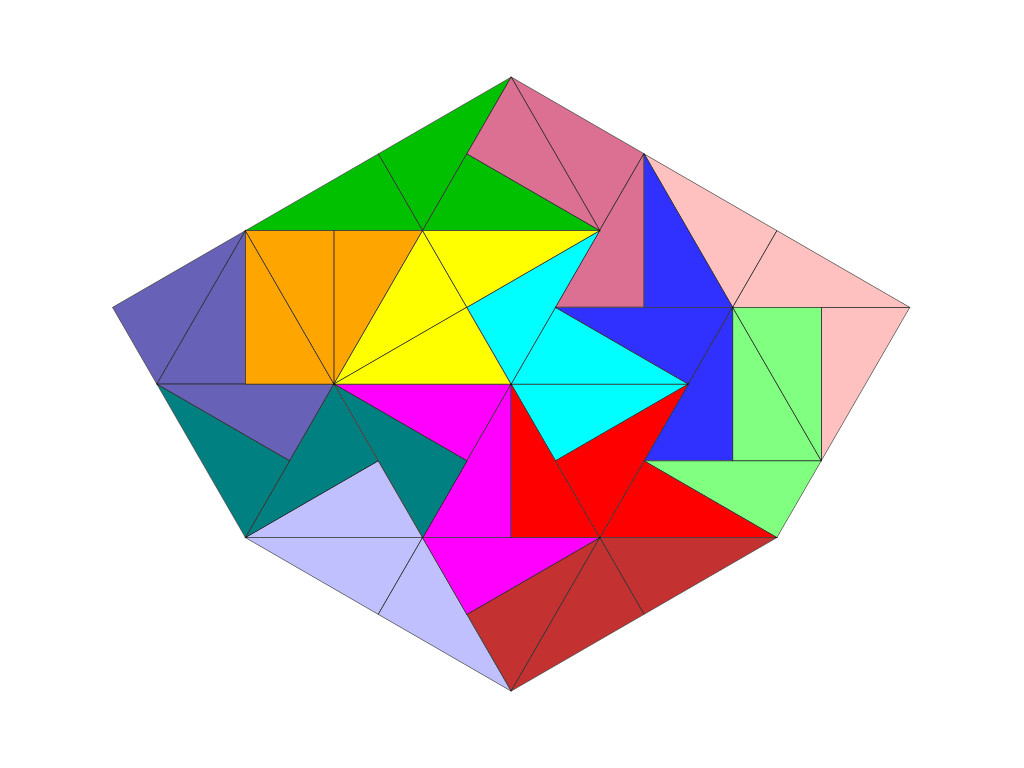
Die Drafter-Figuren „Sägeblatt“ und „Samurai“ haben ausschließlich nicht gitterkonforme Lösungen.

Die 3D-Druckvorlagen bestehen aus den14 Tridraftern und drei Boxen.