Tridrafter — Spielsteine
Die 14 Tridrafter gehören zur Familie der Polydrafter. Einen Monodrafter oder kurz Drafter erhält man durch Halbieren eines gleichseitigen Dreiecks. Der Monodrafter ist ein Dreieck mit 30°, 60° und 90°-Innenwinkeln.
Die Tridrafter fügen sich in das Dreiecksgitter ein. Es gibt auch andere Sets aus verbundenen Draftern, zum Beispiel die Pentadrafter, die in ein Draftergitter passen. Sie sollen jedoch an dieser Stelle nicht betrachtet werden.
Puzzles aus Tridraftern
Symmetrien
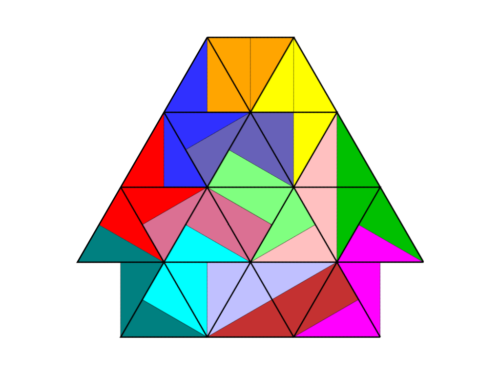
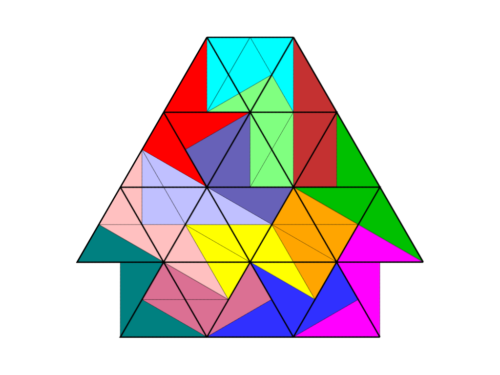
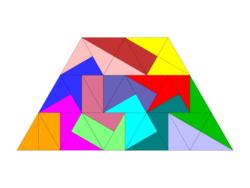
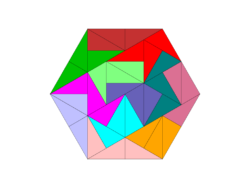
Figuren aus 14 Tridraftern bestehen aus 42 Dreiecken. Das zugrundeliegende Dreiecksgitter lässt Figuren mit 6 Spiegelachsen und 6‑facher Drehsymmetrie zu. Eine Figur mit maximaler Symmetrie aus 12 Spielsteinen ist zum Beispiel das unten abgebildete Hexagon. Eine Figur aus allen 14 Tridraftern mit maximaler Symmetrie ist nicht bekannt. Die Figur “Sägeblatt” ist immerhin 6‑fach drehsymmetrisch.
Allen Figuren, bestehend aus 14 Tridraftern ist gemeinsam, dass sie nur wenige Lösungen besitzen. Der Schwierigkeitsgrad der Puzzle ist hoch und liegt irgendwo zwischen sehr schwierig und unlösbar (für einen Menschen).
Gitterkonformität
Die 14 Tridrafter fügen sich in ein Gitter aus gleichseitigen Dreiecken ein. Sie verhalten sich “gitterkonform”. Für Figuren, die aus Tridraftern erstellt werden, gilt das allerdings selten. In den meisten Lösungen halten sich die Spielsteine nicht an die vorgegebene Gitterstruktur — es gibt “Gittersprünge”. Die zwei folgenden Abbildungen zeigen eine Figur mit einer gitterkonformen und einer nicht gitterkonformen Lösung.
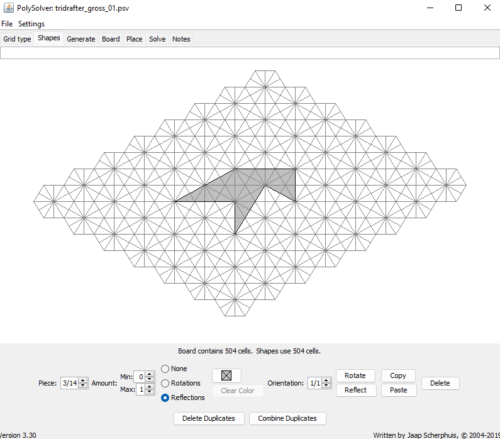
Beim Erstellen der Tridrafter-Spielsteine im Lösungsprogramm Polysolver muss man dies beachten. Erstellt man die Tridrafter jeweils aus 9 Dreiecken (Abbildung 1), erhält man nur gitterkonforme Lösungen. Hingegen erhält man durch die Verwendung von 36 Dreiecken pro Spielstein alle möglichen Lösungen (Abbildung 2). Eine Figur, die aus allen 14 Tridraftern besteht, setzt sich somit aus insgesamt 504 Dreiecken zusammen.
Mehr Infos zu Gitterkonformität und Gittersprüngen gibt es auf Logelium.
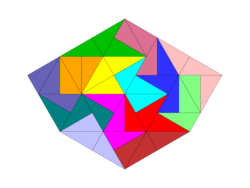
Einige Tridrafter-Figuren
Was findet man auf dieser Webseite?
externe Links