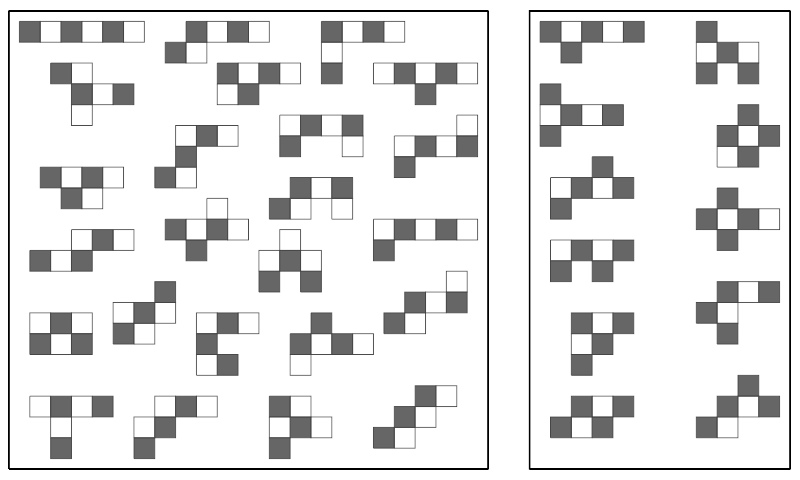
Hexominoes – The Puzzle Pieces
Each of the 35 hexominoes is made up of 6 squares. They belong to the family of polyominoes.
If cubes are used instead of squares, three-dimensional shapes can be constructed—just like with the better-known pentominoes.

Puzzles made of Hexominoes



The 3D print templates include three puzzles. They consist of 6, 10, and 36 hexominoes respectively (one hexomino is printed twice).
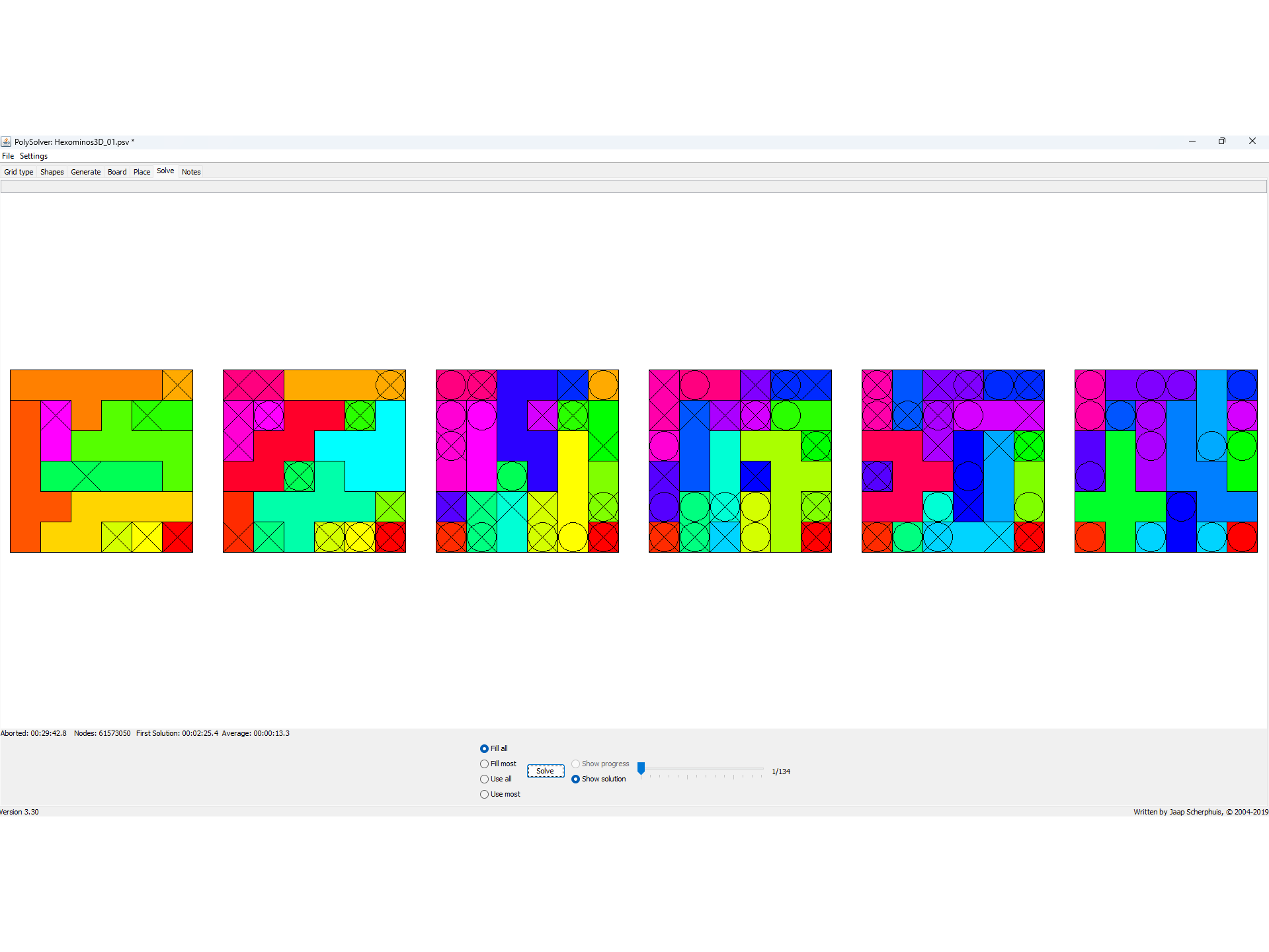
The puzzles were solved using the program PolySolver.
Some figures made from hexominoes








Rectangles made from hexominoes
Since each hexomino consists of six unit squares, one might expect that it would be possible to form various rectangles without gaps (so-called compact rectangles). However, this turns out to be impossible, as can be demonstrated with a rectangle of size 21 × 10.
If all 35 hexominoes are colored in a checkerboard pattern (see image on the right), two types of tiles can be distinguished:
- 24 odd hexominoes, each consisting of exactly 3 black and 3 white squares.
- 11 even hexominoes, with a color distribution of either 4 : 2 or 2 : 4.
The odd hexominoes together make up 72 black and 72 white squares. The even ones also result in an even number of black and white squares overall.
Thus, the complete set of 35 hexominoes contains an even number of black and white squares.
Now, if the 21 × 10 rectangle is also colored in a checkerboard pattern (see right image), it contains 105 black and 105 white squares — both odd numbers.
Because an even number of black and white fields (from the hexominoes) cannot be mapped onto a pattern with an odd number of black and white fields, a gapless tiling of the rectangle is impossible.
Since this parity argument applies to any rectangle with 210 unit squares, no compact rectangle exists that can be completely filled using all 35 hexominoes.

Resources & Downloads
3D Printing Templates
33D printing templates for 3 puzzles
The 3D-printed hexominoes use cubes instead of squares as their basic building blocks. They can also be regarded as a selection of hexacubes, which allows the construction of three-dimensional figures.