Tridrafter – The Pieces
Tridrafter in the Triangular Grid
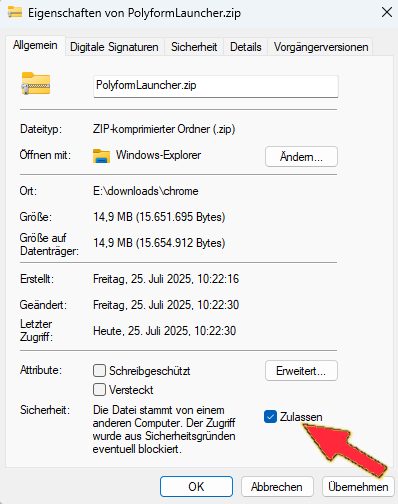
A monodrafter – or simply drafter – is a right triangle with interior angles of 30°, 60°, and 90°. Connected drafters form polydrafters. The possible sets of these polydrafters depend on the underlying grid. The tridrafters considered here fit into the triangular grid.
When forming polyforms, it is generally assumed that two base shapes must connect along their full edge length. Because a drafter’s shorter leg is only half as long as its hypotenuse, this rule can be extended: a connection along half the hypotenuse is also regarded as valid. This extension allows for additional connection variants – including those used for the tridrafters discussed here.
With these two rules, the resulting counts are: 6 didrafters, 14 tridrafters, 64 tetradrafters, 237 pentadrafters, and 1025 hexadrafters.

Tridrafter-Puzzles
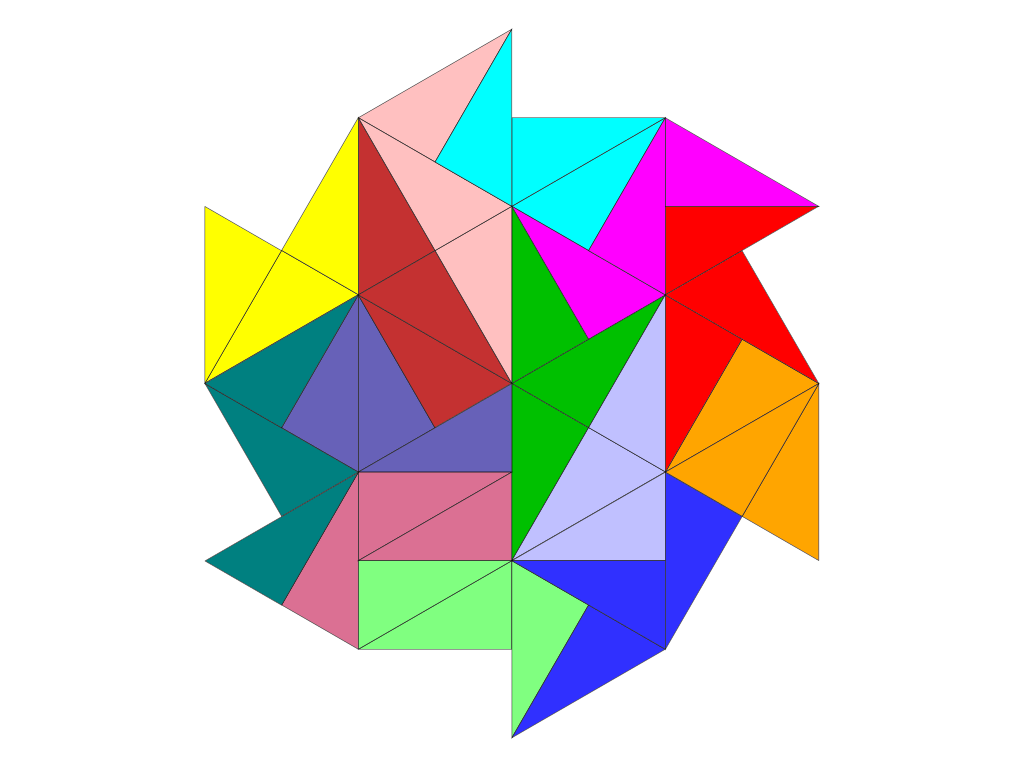
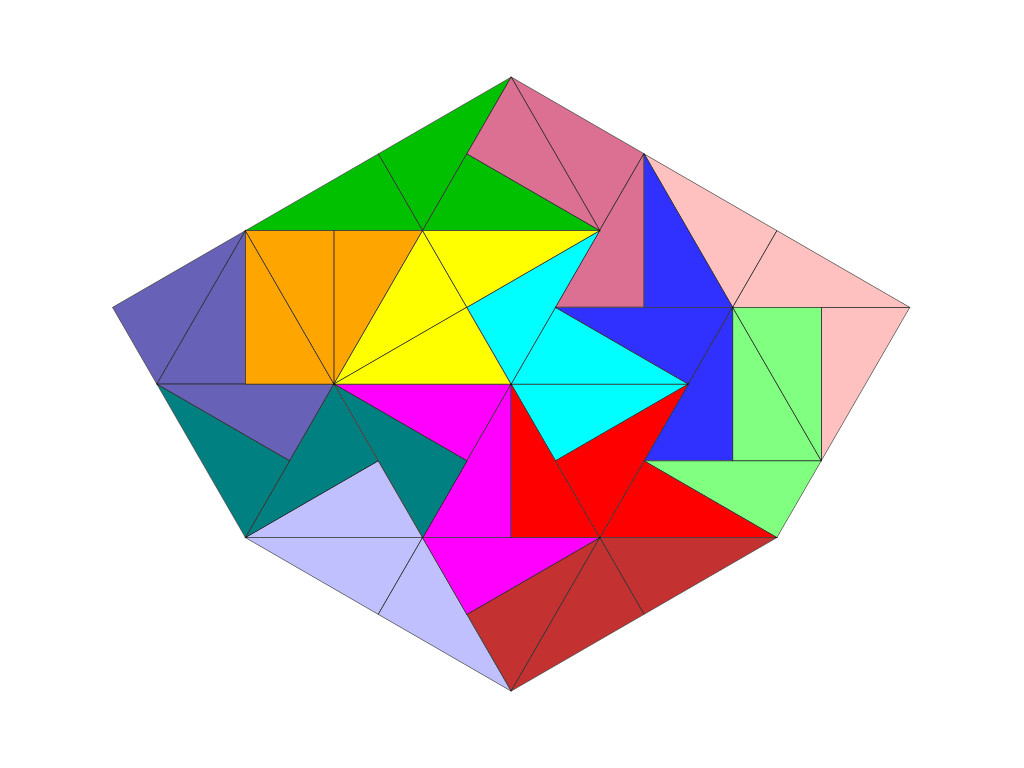
Tridrafter – Shapes and Symmetries
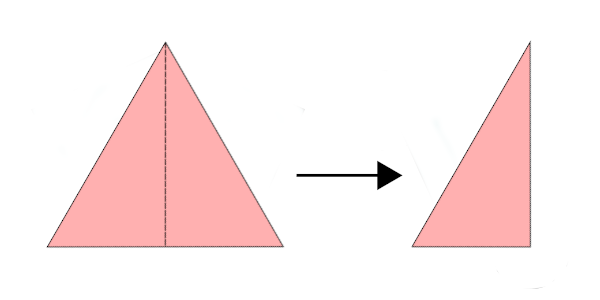
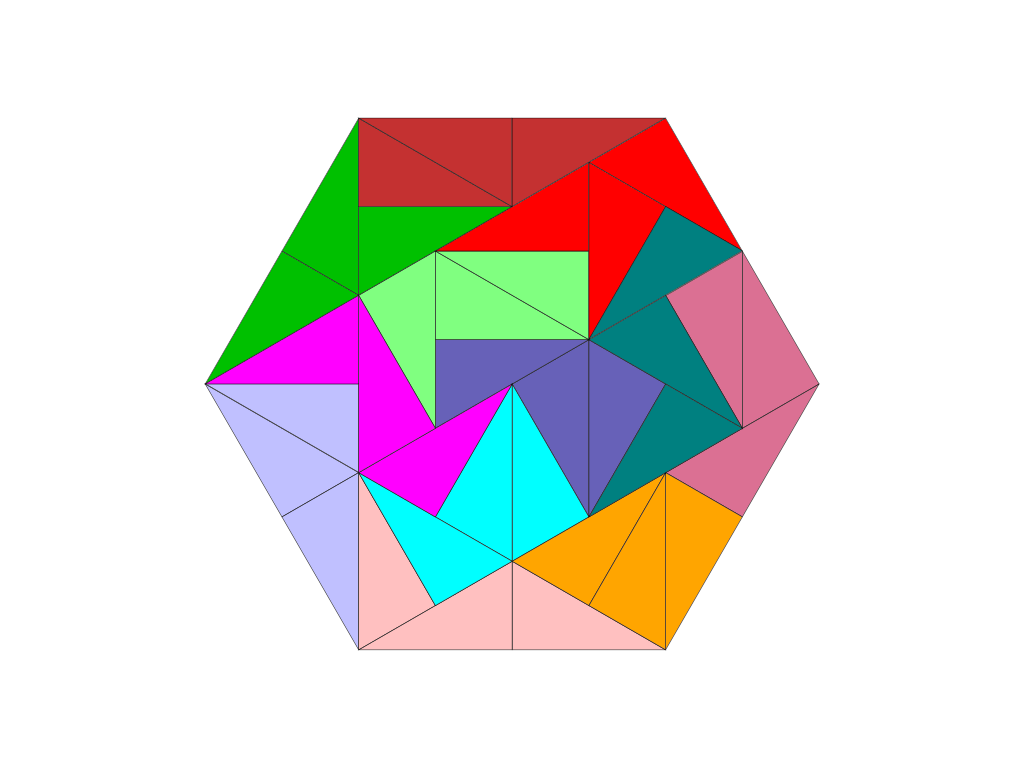
Shapes made from 14 tridrafters cover an area of 42 triangles.
The underlying triangular grid permits shapes with six lines of reflection and six-fold rotational symmetry. A shape with maximum symmetry that uses only 12 pieces is, for example, the hexagon shown below. A fully symmetric shape that incorporates all 14 tridrafters is not yet known. The “saw blade” shape, however, does exhibit six-fold rotational symmetry.
All shapes composed of the 14 tridrafters share one property: they allow only very few possible solutions. The difficulty level of such puzzles is high and—at least for a human solver—ranges from “very difficult” to “virtually unsolvable.”
Further information on tridrafters can be found on Logelium.
Grid Conformity
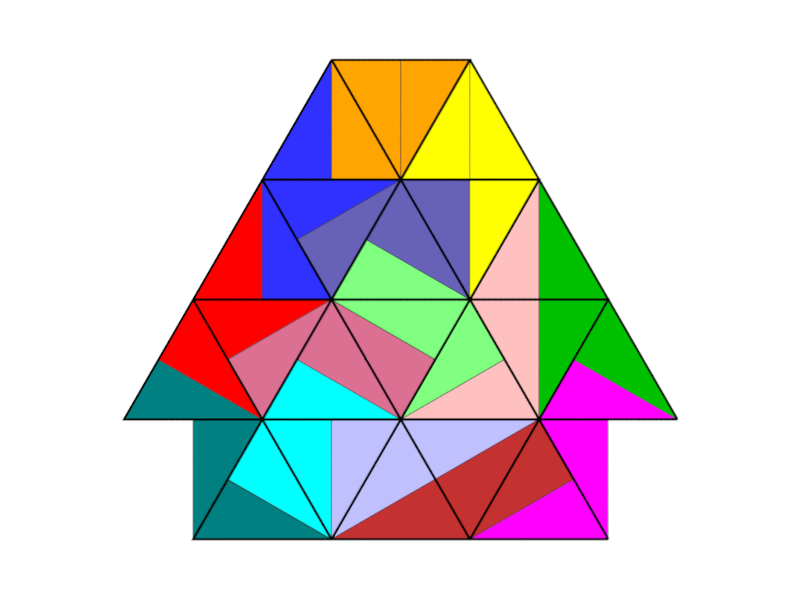
The 14 tridrafters fit into a grid of equilateral triangles; in this sense they exhibit “grid conformity”. However, this property rarely carries over to shapes assembled from these pieces. In most solutions, the tridrafters do not consistently follow the underlying grid structure—resulting in what can be described as “grid shifts”.
The two illustrations show, by example, one grid-conforming shape and one non-grid-conforming shape.
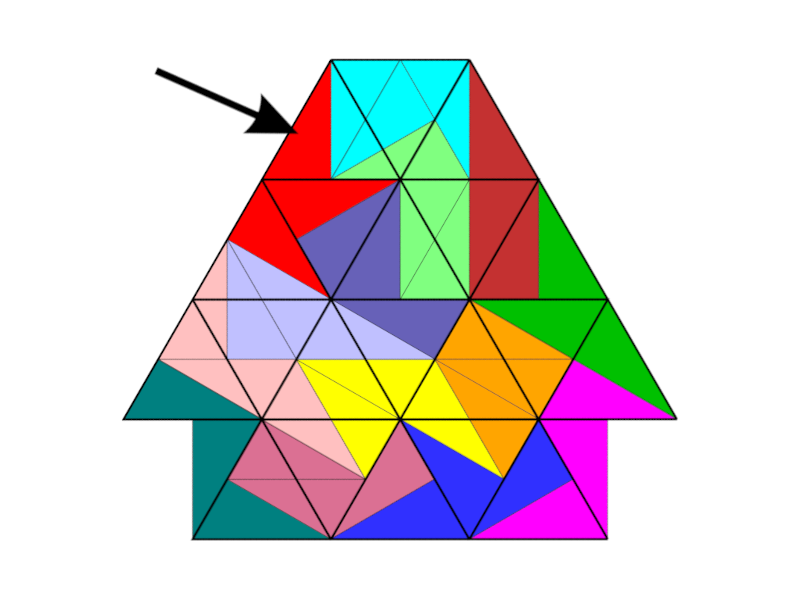
Solution Programs and Grid Conformity
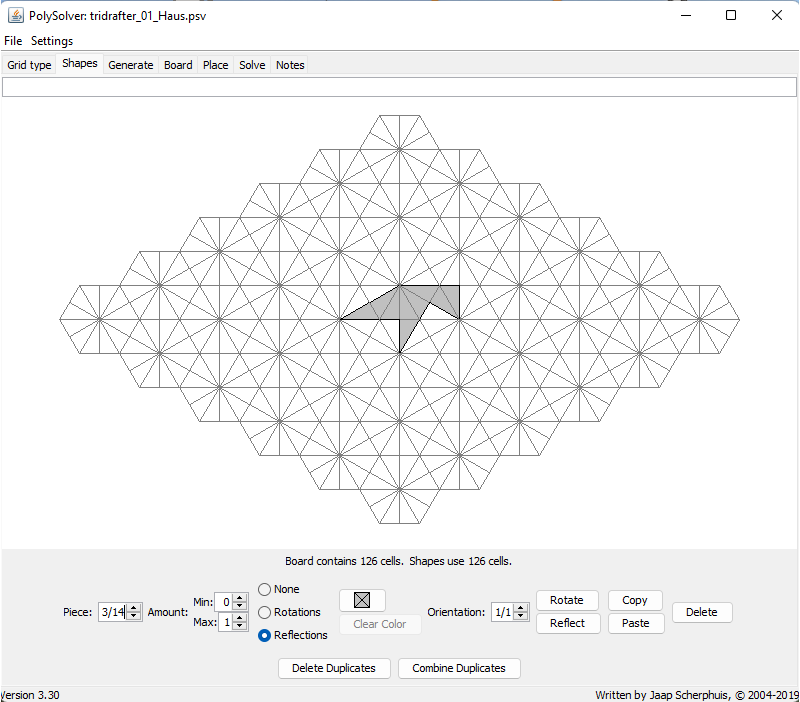
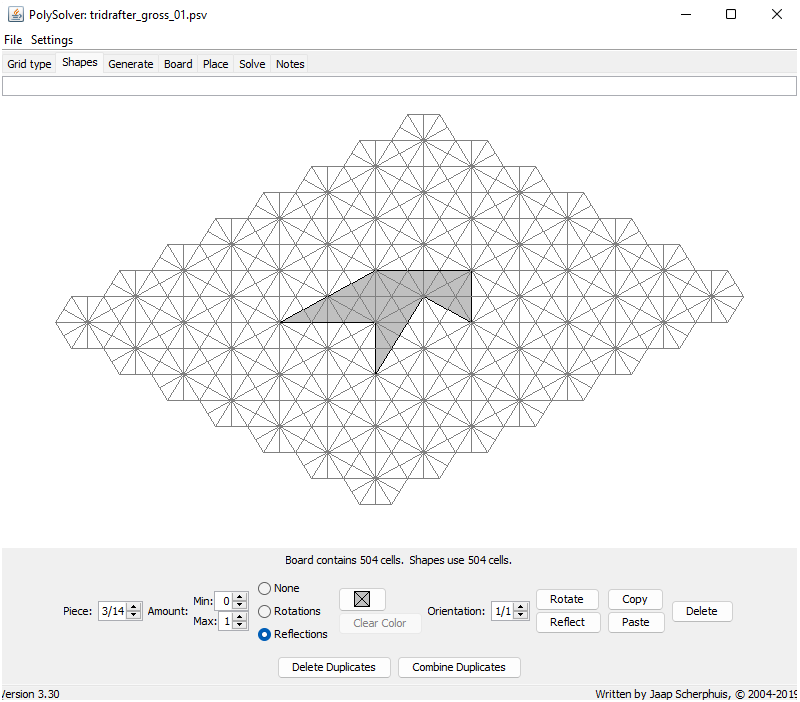
This distinction between grid-conforming and non–grid-conforming shapes is particularly relevant when using solution software.
When creating the Tridrafter pieces in the PolySolver program, the choice of internal structure affects the types of possible solutions. If each piece is built from 9 triangles (see Figure 1), only grid-conforming solutions arise. Using 36 triangles per piece (see Figure 2), however, allows solutions with grid shifts. A shape that includes all 14 Tridrafters then consists of a total of 504 triangles in this representation.
The Drafter shapes “Saw Blade” and “Samurai” have exclusively non–grid-conforming solutions.
Some Tridrafter Shapes









Resources & Downloads
3D Print Templates
The 3D-print templates consist of the 14 Tridrafter puzzle pieces and three boxes.